Simple Harmonic Motion 3 Question 9
9. A uniform cylinder of length
(a)
(b)
(c)
(d)
Analytical & Descriptive Questions
Show Answer
Answer:
Correct Answer: 9. (b)
Solution:
- When cylinder is displaced by an amount
Net restoring force
or
or
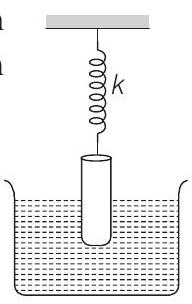
Now,






