Simple Harmonic Motion 3 Question 8
8. A highly rigid cubical block
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 8. (d)
Solution:
- Modulus of rigidity,
Here,
and
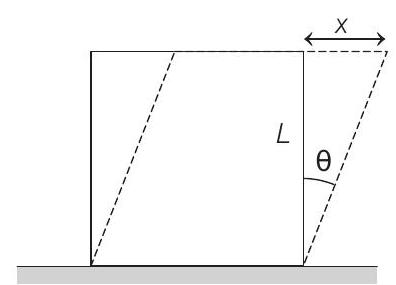
Therefore, restoring force is
or acceleration,
Since,






