Simple Harmonic Motion 3 Question 7
7. One end of a long metallic wire of length $L$ is tied to the ceiling. The other end is tied to a massless spring of spring constant $k$. A mass $m$ hangs freely from the free end of the spring. The area of cross-section and the Young’s modulus of the wire are $A$ and $Y$ respectively. If the mass is slightly pulled down and released, it will oscillate with a time period $T$ equal to
(1993, 2M)
(a) $2 \pi(m / k)^{1 / 2}$
(b) $2 \pi \sqrt{\frac{m(Y A+k L)}{Y A k}}$
(c) $2 \pi\left[(m Y A / k L)^{1 / 2}\right.$
(d) $2 \pi(m L / Y A)^{1 / 2}$
Show Answer
Answer:
Correct Answer: 7. (b)
Solution:
- $k _{eq}=\frac{k _1 k _2}{k _1+k _2}=\frac{\frac{Y A}{L}}{\frac{Y A}{L}+k}=\frac{Y A k}{Y A+L k}$
$$ \begin{aligned} & \begin{aligned} \therefore \quad T & =2 \pi \sqrt{\frac{m}{k _{eq}}} \\ & =2 \pi \sqrt{\frac{m(Y A+L k)}{Y A k}} \end{aligned} \end{aligned} $$
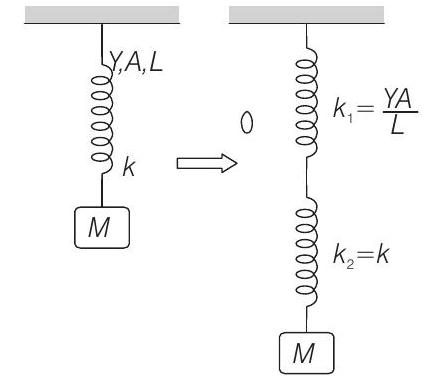
NOTE Equivalent force constant for a wire is given by $k=\frac{Y A}{L}$. Because in case of a wire, $F=\frac{Y A}{L} \Delta L$ and in case of spring , $F=k . \Delta x$. Comparing these two, we find $k$ of wire $=\frac{Y A}{L}$.
