Rotation 5 Question 5
14. A thin uniform $\operatorname{rod}$, pivoted at $O$, is rotating in the horizontal plane with constant angular speed $\omega$, as shown in the figure. At time $t=0$, a small insect starts from $O$ and moves with constant speed $v$ with respect to the rod towards the other end. It reaches the end of the rod at $t=T$ and stops. The angular speed of the system remains $\omega$ throughout.
(2012)
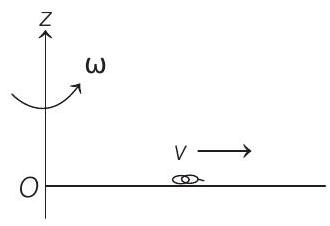
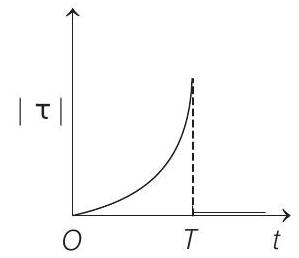
The magnitude of the torque $|\tau|$ on the system about $O$, as a function of time is best represented by which plot? (a)
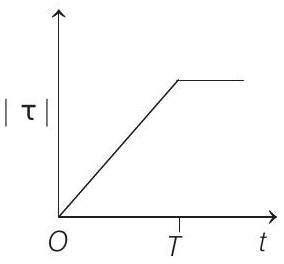
(c)
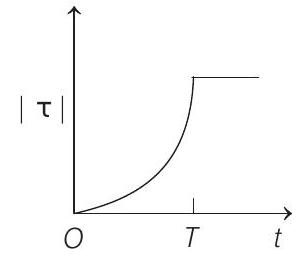
(b)
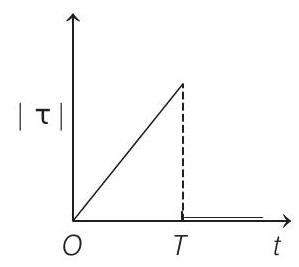
(d)
Show Answer
Answer:
Correct Answer: 14. (b)
Solution:
- $|\mathbf{L}|$ or $L=I \omega$ (about axis of rod)
$$ I=I _{rod}+m x^{2}=I _{rod}+m v^{2} t^{2} $$
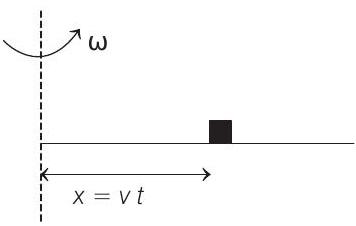
Here, $m=$ mass of insect
$\therefore \quad L=\left(I _{\text {rod }}+m v^{2} t^{2}\right) \omega$
Now $|\tau|=\frac{d L}{d t}=\left(2 m v^{2} t \omega\right) \quad$ or $\quad|\tau| \propto t$
i.e. the graph is straight line passing through origin.
After time $T, L=$ constant
$$ \therefore \quad|\tau| \text { or } \frac{d L}{d t}=0 $$
