Rotation 5 Question 29
41. A block $X$ of mass $0.5 kg$ is held by a long massless string on a frictionless inclined plane of inclination $30^{\circ}$ to the horizontal. The string is wound on a uniform solid cylindrical drum $Y$ of mass $2 kg$ and of radius $0.2 m$ as shown in figure.
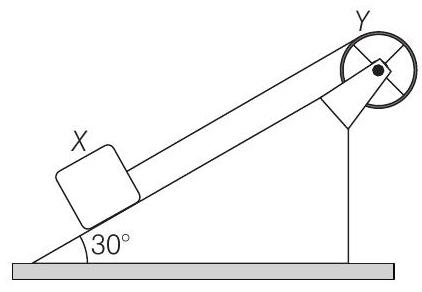
The drum is given an initial angular velocity such that the block $X$ starts moving up the plane.
$(1994,6$ M)
(a) Find the tension in the string during the motion.
(b) At a certain instant of time, the magnitude of the angular velocity of $Y$ is $10 rads^{-1}$. Calculate the distance travelled by $X$ from that instant of time until it comes to rest.
Show Answer
Answer:
Correct Answer: 41. (a) $1.63 N$
(b) $1.22 m$
Solution:
- Given, mass of block $X, m=0.5 kg$
Mass of drum $Y, \quad M=2 kg$
Radius of drum, $\quad R=0.2 m$
Angle of inclined plane, $\theta=30^{\circ}$
(a) Let $a$ be the linear retardation of block $X$ and $\alpha$ be the angular retardation of $\operatorname{drum} Y$. Then, $a=R \alpha$
$$ m g \sin 30^{\circ}-T=m a $$
or
$$ \begin{aligned} \frac{m g}{2}-T & =m a \\ \alpha=\frac{\tau}{I} & =\frac{T R}{\frac{1}{2} M R^{2}} \\ \alpha & =\frac{2 T}{M R} \end{aligned} $$
or
Solving Eqs. (i), (ii) and (iii) for $T$, we get,
$$ T=\frac{1}{2} \frac{M m g}{M+2 m} $$
Substituting the value, we get
$$ T=\frac{1}{2} \frac{(2)(0.5)(9.8)}{2+(0.5)(2)}=1.63 N $$
(b) From Eq. (iii), angular retardation of drum
$$ \alpha=\frac{2 T}{M R}=\frac{(2)(1.63)}{(2)(0.2)}=8.15 rad / s^{2} $$
or linear retardation of block
$$ a=R \alpha=(0.2)(8.15)=1.63 m / s^{2} $$
At the moment when angular velocity of drum is
$$ \omega _0=10 rad / s $$
The linear velocity of block will be
$$ v _0=\omega _0 R=(10)(0.2)=2 m / s $$
Now, the distance $(s)$ travelled by the block until it comes to rest will be given by
$$ \begin{aligned} s & =\frac{v _0^{2}}{2 a} \quad\left(\text { Using } v^{2}=v _0^{2}-2 a s \text { with } v=0\right) \\ & =\frac{(2)^{2}}{2(1.63)} \text { or } s=1.22 m \end{aligned} $$
