SATHEE: Rotation 5 Question 28

Rotation 5 Question 28

40. A rectangular rigid fixed block has a long horizontal edge. A solid homogeneous cylinder of radius $R$ is placed horizontally at rest with its length parallel to the edge such that the axis of the cylinder and the edge of the block are in the same vertical plane as shown in figure. There is sufficient friction present at the edge, so that a very small displacement causes the cylinder to roll off the edge without slipping. Determine

(1995, 10M)

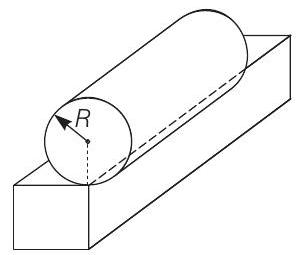
(a) the angle $θ_{c}$ through which the cylinder rotates before it leaves contact with the edge, (b) the speed of the centre of mass of the cylinder before leaving contact with the edge and

(c) the ratio of the translational to rotational kinetic energies of the cylinder when its centre of mass is in horizontal line with the edge.

Show Answer

Answer:

Correct Answer: 40. (a) $θ = \cos^{- 1} \frac{4}{7}$

(b) $\sqrt{\frac{4 g R}{7}}$

Solution:

(a) The cylinder rotates about the point of contact. Hence, the mechanical energy of the cylinder will be conserved i.e.

$∴ (P E + K E)_{1} = (P E + K E)_{2}$

$∴ m g R + 0 = m g R \cos θ + \frac{1}{2} I ω^{2} + \frac{1}{2} m v^{2}$

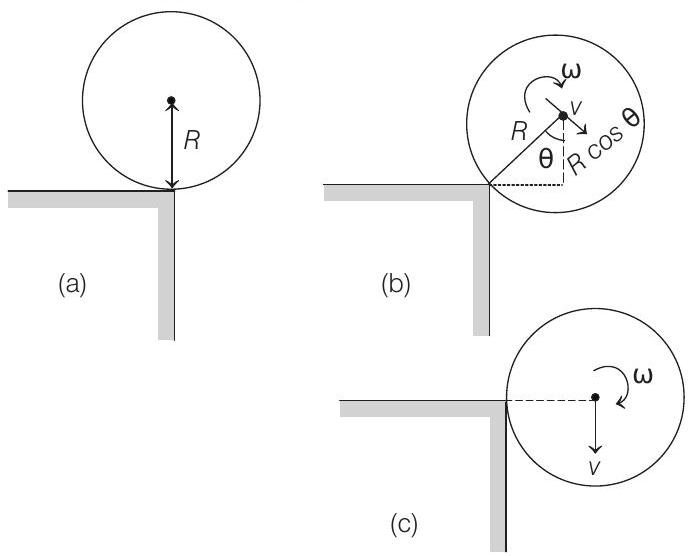
but $ω = v / R$ (no slipping at point of contact)

$and I = \frac{1}{2} m R^{2}$

Therefore,

$m g R = m g R \cos θ + \frac{1}{2} \frac{1}{2} m R^{2} \frac{v^{2}}{R^{2}} + \frac{1}{2} m v^{2}$

or $\frac{3}{4} v^{2} = g R (1 - \cos θ)$

$\begin{aligned} v^{2} & = \frac{4}{3} g R (1 - \cos θ) \\ \frac{v^{2}}{R} & = \frac{4}{3} g (1 - \cos θ) \end{aligned}$

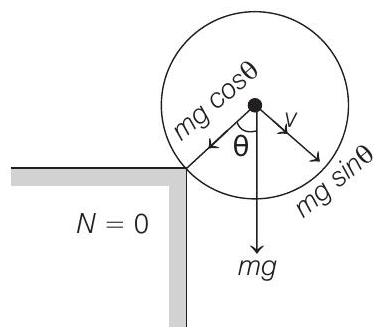
At the time of leaving contact, normal reaction $N = 0$ and $θ = θ_{c .}$ . hence,

$m g \cos θ = \frac{m v^{2}}{R} or \frac{v^{2}}{R} = g \cos θ$

From Eqs. (i) and (ii),

$\frac{4}{3} g (1 - \cos θ_{c}) = g \cos θ_{c}$

or $\frac{7}{4} \cos θ_{c} = 1$ or $\cos θ_{c} = 4 / 7$ or $θ_{c} = \cos^{- 1} (4 / 7)$

(b) $v = \sqrt{\frac{4}{3} g R (1 - \cos θ)}$

At the time of losing contact

$\begin{aligned} \cos θ & = \cos θ_{c} = 4 / 7 \\ ∴ v & = \sqrt{\frac{4}{3} g R 1 - \frac{4}{7}} or v = \sqrt{\frac{4}{7} g R} \end{aligned}$

Therefore, speed of CM of cylinder just before losing contact is $\sqrt{\frac{4}{7} g R}$

$v = \sqrt{\frac{4}{7} g R}$

Therefore, rotational kinetic energy, $K_{R} = \frac{1}{2} I ω^{2}$

$\begin{array}{ll} or & K_{R} = \frac{1}{2} \frac{1}{2} m R^{2} \frac{v^{2}}{R^{2}} = \frac{1}{4} m v^{2} = \frac{1}{4} m \frac{4}{7} g R \\ or K_{R} = \frac{m g R}{7} \end{array}$

Now, once the cylinder loses its contact, $N = 0$ , i.e the frictional force, which is responsible for its rotation, also vanishes. Hence, its rotational kinetic energy now becomes constant, while its translational kinetic energy increases. Applying conservation of energy at (a) and (c).

Decrease in gravitational PE

$=$ Gain in rotational $K E +$ translational $K E$