Rotation 5 Question 27
39. A uniform disc of mass $m$ and radius $R$ is projected horizontally with velocity $v _0$ on a rough horizontal floor, so that it starts off with a purely sliding motion at $t=0$. After $t _0$ seconds, it acquires a purely rolling motion as shown in figure.
(1997 C, 5M)
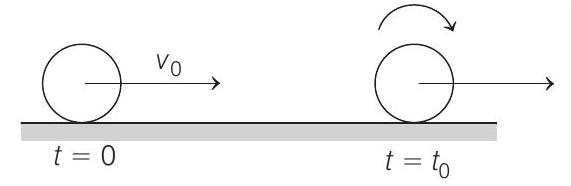
(a) Calculate the velocity of the centre of mass of the disc at $t _0$.
(b) Assuming the coefficient of friction to be $\mu$, calculate $t _0$. Also calculate the work done by the frictional force as a function of time and the total work done by it over a time $t$ much longer than $t _0$.
Show Answer
Answer:
Correct Answer: 39. (a) $\frac{2}{3} v_0$
(b) $\frac{v_0}{3 \propto g}$, For $t \leq t_0, W_f=\frac{m \propto g t}{2}\left[3 \propto g t-2 v_0\right], \frac{-m v_0^2}{6}$
Solution:
- (a) Between the time $t=0$ to $t=t _0$. There is forward sliding, so friction $f$ is leftwards and maximum i.e. $\mu m g$. For time $t>t _0$, friction $f$ will become zero, because now pure rolling has started i.e. there is no sliding (no relative motion) between the points of contact.
So, for time $t<t _0$
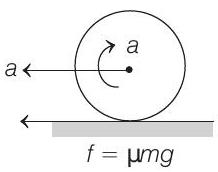
Linear retardation, $a=\frac{f}{m}=\mu g$
and angular acceleration, $\alpha=\frac{\tau}{I}=\frac{f R}{\frac{1}{2} m R^{2}}=\frac{2 \mu g}{R}$
Now, let $v$ be the linear velocity and $\omega$, the angular velocity of the disc at time $t=t _0$, then
$$ v=v _0-a t _0=v _0-\mu g t _0 $$
and
$$ \omega=\alpha t _0=\frac{2 \mu g t _0}{R} $$
For pure rolling to take place
$$ v=R \omega $$
i.e. $\quad v _0-\mu g t _0=2 \mu g t _0 \Rightarrow t _0=\frac{v _0}{3 \mu g}$
Substituting in Eq. (i), we have
$$ v=v _0-\mu g \quad \frac{v _0}{3 \mu g} \Rightarrow v=\frac{2}{3} v _0 $$
(b) Work done by friction
For $t \leq t _0$, linear velocity of disc at any time $t$ is $v=v _0-\mu g t$ and angular velocity is $\omega=\alpha t=\frac{2 \mu g t}{R}$. From Work-energy theorem, work done by friction upto time $t=$ Kinetic energy of the disc at time $t$ - Kinetic energy of the disc at time $t=0$
$\therefore \quad W=\frac{1}{2} m v^{2}+\frac{1}{2} I \omega^{2}-\frac{1}{2} m v _0^{2}$
$=\frac{1}{2} m\left[v _0-\mu g t\right]^{2}+\frac{1}{2} \frac{1}{2} m R^{2} \quad \frac{2 \mu g t^{2}}{R} \quad-\frac{1}{2} m v _0^{2}$
$=\frac{1}{2}\left[m v _0^{2}+m \mu^{2} g^{2} t^{2}-2 m v _0 \mu g t+2 m \mu^{2} g^{2} t^{2}-m v _0^{2}\right]$
or $W=\frac{m \mu g t}{2}\left[3 \mu g t-2 v _0\right]$
For $t>t _0$, friction force is zero i.e. work done in friction is zero. Hence, the energy will be conserved.
Therefore, total work done by friction over a time $t$ much longer then $t _0$ is total work done upto time $t _0$ (because beyond this work done by friction is zero) which is equal to
$$ W=\frac{m \mu g t _0}{2}\left[3 \mu g t _0-2 v _0\right] $$
Substituting $t _0=v _0 / 3 \mu g$,we get
$$ W=\frac{m v _0}{6}\left[v _0-2 v _0\right] \Rightarrow W=-\frac{m v _0^{2}}{6} $$
