SATHEE: Rotation 5 Question 24

Rotation 5 Question 24

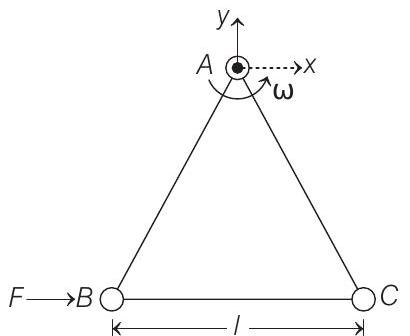36. Three particles $A, B$ and $C$ , each of mass $m$ , are connected to each other by three massless rigid rods to form a rigid, equilateral triangular body of side $l$ . This body is placed on a horizontal frictionless table $(x - y$ plane $)$ and is hinged to

it at the point $A$ , so that it can move without friction about the vertical axis through $A$ (see figure). The body is set into rotational motion on the table about $A$ with a constant angular velocity $ω$ .

(2002, 5M)

(a) Find the magnitude of the horizontal force exerted by the hinge on the body.

(b) At time $T$ , when the side $B C$ is parallel to the $X$ -axis, a force $F$ is applied on $B$ along $B C$ (as shown). Obtain the $x$ -component and the $y$ -component of the force exerted by the hinge on the body, immediately after time $T$ .

Show Answer

Answer:

Correct Answer: 36. (a) $\sqrt{3} m l ω^{2}$

(b) ${(F_{net})}_{x} = \frac{- F}{4}, {(F_{net})}_{y} = \sqrt{3} m l ω^{2}$

Solution:

(a) The distance of centre of mass (CM) of the system about point $A$ will be $r = \frac{l}{\sqrt{3}}$

Therefore, the magnitude of horizontal force exerted by the hinge on the body is

$F =$ centripetal force or $F = (3 m) r ω^{2}$

$\begin{aligned} or \\ F = (3 m) \frac{l}{\sqrt{3}} ω^{2} \\ or \\ F = \sqrt{3} m l ω^{2} \end{aligned}$

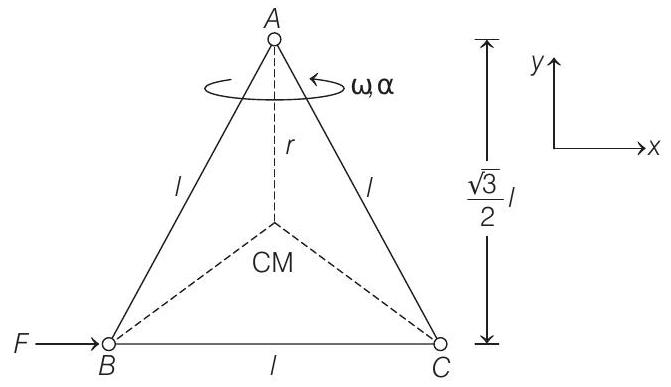
(b) Angular acceleration of system about point $A$ is

$α = \frac{τ_{A}}{I_{A}} = \frac{(F) \frac{\sqrt{3}}{2} l}{2 m l^{2}} = \frac{\sqrt{3} F}{4 m l}$

Now, acceleration of CM along $x$ -axis is

$a_{x} = r α = \frac{l}{\sqrt{3}} \frac{\sqrt{3} F}{4 m l} or a_{x} = \frac{F}{4 m}$

Let $F_{x}$ be the force applied by the hinge along $X$ -axis.

$\begin{aligned} Then, & F_{x} + F & = (3 m) a_{x} \\ or & F_{x} + F & = (3 m) \frac{F}{4 m} \\ or & F_{x} + F & = \frac{3}{4} F \\ or & F_{x} & = - \frac{F}{4} \end{aligned}$