SATHEE: Rotation 5 Question 13

Rotation 5 Question 13

23. In the List-I below, four different paths of a particle are given as functions of time. In these functions, $α$ and $β$ are positive constants of appropriate dimensions and $α \neq β$ . In each case, the force acting on the particle is either zero or conservative. In List-II, five physical quantities of the particle are mentioned: $p$ is the linear momentum, $L$ is the angular momentum about the origin, $K$ is the kinetic energy, $U$ is the potential energy and $E$ is the total energy. Match each path in List-I with those quantities in List-II, which are conserved for that path.

(2018 Adv.)

List-I		ist-II
P. $r (t) = α t i + β t j$	1.	$p$
Q. $r (t) = α \cos ω t i + β \sin ω t j$	2.	L
R. $r (t) = α (\cos ω t i + \sin ω t j)$	3.	K
S. $r (t) = a t i + \frac{β}{2} t^{2} j$	4.	$U$
	5.	$E$

(a) $P \to 1, 2, 3, 4, 5; Q \to 2, 5; R \to 2, 3, 4, 5; S \to 5$

(b) $P \to 1, 2, 3, 4, 5$ ; $\to$ 3, 5; R $\to 2, 3, 4, 5; S \to 2, 5$

(d) $P \to 1, 2, 3, 5; Q \to 2, 5; R \to 2, 3, 4, 5; S \to 2, 5$

Passage Based Questions

Passage 1

One twirls a circular ring (of mass 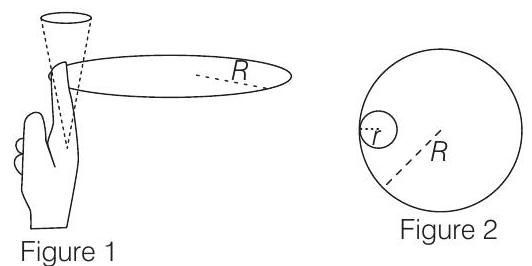$M$ and radius $R$ ) near the tip of one’s finger as shown in Figure 1. In the process the finger never loses contact with the inner rim of the ring. The finger traces out the surface of a cone, shown by the dotted line. The radius of the path traced out by the point where the ring and the finger is in contact is $r$ . The finger rotates with an angular velocity $ω_{0}$ . The rotating ring rolls without slipping on the outside of a smaller circle described by the point where the ring and the finger is in contact (Figure 2). The coefficient of friction between the ring and the finger is $μ$ and the acceleration due to gravity is $g$ .

Show Answer

Answer:

Correct Answer: 23. (a)

Solution:

When force $F = 0 \Rightarrow$ potential energy $U =$ constant $F \neq 0 \Rightarrow$ force is conservative $\Rightarrow$ Total energy $E =$ constant List-I

(P) $r (t) = α t \hat{i} + β t \hat{j}$

$\begin{aligned} \frac{d r}{d t} & = v = α \hat{i} + β \hat{j} = constant \Rightarrow p = constant \\ | v | & = \sqrt{α^{2} + β^{2}} = constant \Rightarrow K = constant \\ \frac{d v}{d t} & = a = 0 \Rightarrow F = 0 \Rightarrow U = constant \\ E & = U + K = constant \\ L & = m (r \times v) = 0 \\ L & = constant \end{aligned}$

$P \to 1, 2, 3, 4, 5$

(Q) $r (t) = α \cos ω t \hat{i} + β \sin ω t \hat{j}$

$\frac{d r}{d t} = v = α ω \sin ω t (\hat{i}) + β ω \cos ω t \hat{j} \neq constant$

$\Rightarrow p \neq$ constant

$| v | = ω \sqrt{(α \sin ω t)^{2} + (β \cos ω t)^{2}} \neq constant$

$\Rightarrow K \neq$ constant

$\begin{aligned} a = \frac{d v}{d t} = - ω^{2} r \neq 0 \\ \Rightarrow E = constant = K + U \\ But K \neq constant \Rightarrow U \neq constant \\ L = m (r \times v) = m ω α β (\hat{k}) = constant \\ \frac{d r}{d t} = v = α ω [\sin ω t (- \hat{i}) + \cos ω t \hat{j}] ⧸ constant \\ R \to 2, 3, 4, 5 \\ r (t) = α \hat{i} + \frac{β}{2} t^{2} \hat{j} \\ \frac{d r}{d t} = v = α \hat{i} + β \hat{j} \neq constant \Rightarrow p \neq constant \\ | v | = \sqrt{α^{2} + (β t)^{2}} \neq constant \Rightarrow K \neq constant \\ a = \frac{d v}{d t} = β \hat{j} \neq 0 \Rightarrow E = constant = K + U \end{aligned}$