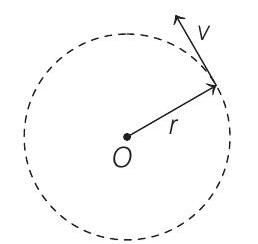
Rotation 5 Question 10
20. The potential energy of mass
(a)
(b)
(c)
(d)
(2018 Adv.)
Show Answer
Answer:
Correct Answer: 20. (b,c)
Solution: