Rotation 5 Question 1
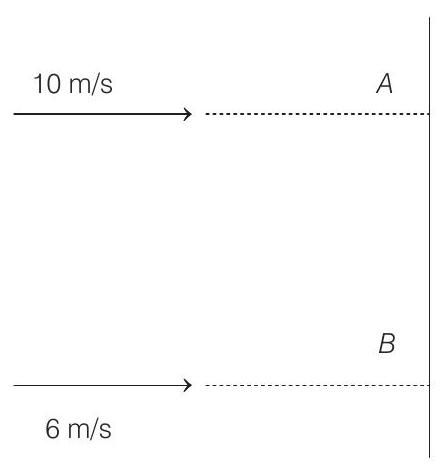
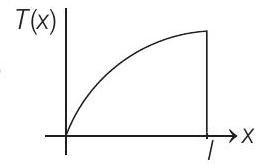
10. A thin uniform bar lies on a frictionless horizontal surface and is free to move in any way on the surface. Its mass is $0.16 kg$ and length is $\sqrt{3} m$. Two particles, each of mass 0.08 $kg$ are moving on the same surface and towards the bar in a direction perpendicular to the bar one with a velocity of 10 $m / s$, and the other with $6 m / s$, as shown in figure. The first particle strikes the bar at points $A$ and the other at point $B$. Points $A$ and $B$ are at a distance of $0.5 m$ from the centre of the bar. The particles strike the bar at the same instant of time and stick to the bar on collision. Calculate the loss of kinetic energy of the system in the above collision process.
(1991)
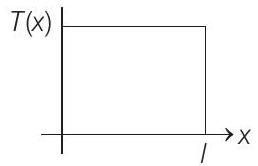
(a)
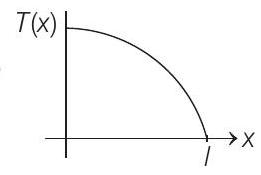
(c)
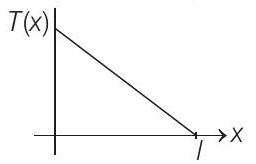
(b)
(d)
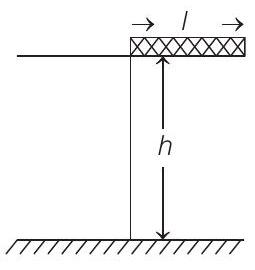
2 A rectangular solid box of length $0.3 m$ is held horizontally, with one of its sides on the edge of a platform of height $5 m$. When released, it slips off the table in a very short time $\tau=0.01 s$, remaining essentially horizontal. The angle by which it would rotate when it hits the ground will be (in radians) close to
(a) 0.02
(b) 0.3
(c) 0.5
(2019 Main, 8 April II)
3 A straight rod of length $L$ extends from $x=a$ to $x=L+a$. The gravitational force it exerts on a point mass $m$ at $x=0$, if the mass per unit length of the $\operatorname{rod}$ is $A+B x^{2}$, is given by
(2019 Main, 12 Jan I)
(a) $G m \quad A \quad \frac{1}{a+L}-\frac{1}{a}-B L$
(b) Gm $A \frac{1}{a+L}-\frac{1}{a}+B L$
(c) $G m \quad A \quad \frac{1}{a}-\frac{1}{a+L}+B L$
(d) $G m \quad A \quad \frac{1}{a}-\frac{1}{a+L}-B L$
4 The magnitude of torque on a particle of mass $1 kg$ is 2.5 $N-m$ about the origin. If the force acting on it is $1 N$ and the distance of the particle from the origin is $5 m$, then the angle between the force and the position vector is (in radian)
(Main 2019, 11 Jan II)
(a) $\frac{\pi}{8}$
(b) $\frac{\pi}{4}$
(c) $\frac{\pi}{3}$
(d) $\frac{\pi}{6}$
5 A slab is subjected to two forces $\mathbf{F} _1$ and $\mathbf{F} _2$ of same magnitude $F$ as shown in the figure. Force $\mathbf{F} _2$ is in $x y$-plane while force $\mathbf{F} _1$ acts along $Z$-axis at the point $(2 \hat{\mathbf{i}}+3 \hat{\mathbf{j}})$. The moment of these forces about point $O$ will be
(2019 Main, 11 Jan I)
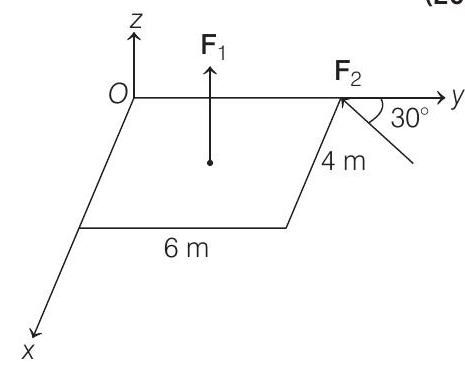
(a) $(3 \hat{\mathbf{i}}+2 \hat{\mathbf{j}}-3 \hat{\mathbf{k}}) F$
(b) $(3 \hat{\mathbf{i}}-2 \hat{\mathbf{j}}+3 \hat{\mathbf{k}}) F$
(c) $(3 \hat{\mathbf{i}}-2 \hat{\mathbf{j}}-3 \hat{\mathbf{k}}) F$
(d) $(3 \hat{\mathbf{i}}+2 \hat{\mathbf{j}}+3 \hat{\mathbf{k}}) F$
6 A rigid massless rod of length $3 l$ has two masses attached at each end as shown in the figure. The rod is pivoted at point $P$ on the horizontal axis (see figure). When released from initial horizontal position, its instantaneous angular acceleration will be
(2019 Main, 10 Jan II)
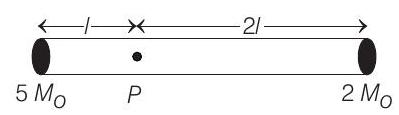
(a) $\frac{g}{13 l}$
(b) $\frac{g}{2 l}$
(c) $\frac{7 g}{3 l}$
(d) $\frac{g}{3 l}$
7 To mop-clean a floor, a cleaning machine presses a circular mop of radius $R$ vertically down with a total force $F$ and rotates it with a constant angular speed about its axis. If the force $F$ is distributed uniformly over the mop and if coefficient of friction between the mop and the floor is $\mu$, the torque applied by the machine on the mop is
(a) $\frac{2}{3} \mu F R$
(b) $\frac{\mu F R}{6}$
(c) $\frac{\mu F R}{3}$
(d) $\frac{\mu F R}{2}$
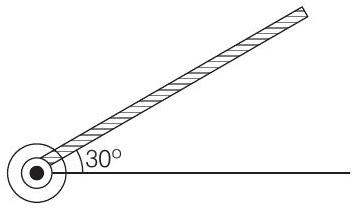
8 A rod of length $50 cm$ is pivoted at one end. It is raised such that if makes an angle of $30^{\circ}$ from the horizontal as shown and released from rest. Its angular speed when it passes through the horizontal (in $rad s^{-1}$ ) will be (Take, $g=10 ms^{-2}$ )
(2019 Main, 09 Jan II)
(a) $\frac{\sqrt{30}}{2}$
(b) $\sqrt{30}$
(c) $\frac{\sqrt{20}}{3}$
(d) $\sqrt{\frac{30}{2}}$
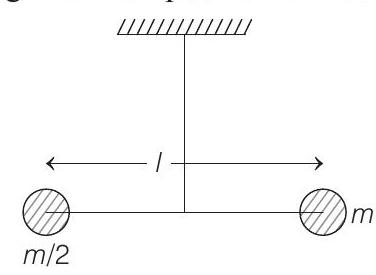
9 Two masses $m$ and $\frac{m}{2}$ are connected at the two ends of a massless rigid rod of length $l$. The rod is suspended by a thin wire of torsional constant $k$ at the centre of mass of the rod-mass system (see figure). Because of torsional constant $k$, the restoring torque is $\tau=k \theta$ for angular displacement $\theta$. If the rod is rotated by $\theta _0$ and released, the tension in it when it passes through its mean position will be (2019 Main, 9 Jan I)
(a) $\frac{2 k \theta _0^{2}}{l}$
(b) $\frac{k \theta _0^{2}}{l}$
(c) $\frac{3 k \theta _0^{2}}{l}$
(d) $\frac{k \Theta _0^{2}}{2 l}$
Show Answer
Answer:
Correct Answer: 10. (a)
Solution:
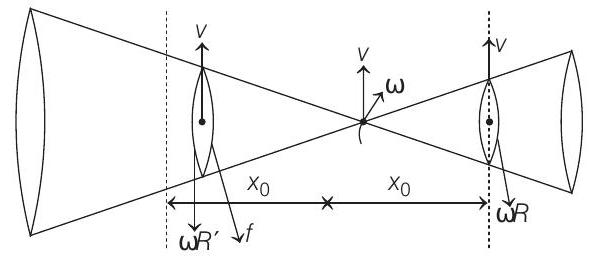
At distance $x _0$ from $O, v=\omega R$
Distance less than $x _0, v>\omega R$
Initially, there is pure rolling at both the contacts. As the cone moves forward, slipping at $A B$ will start in forward direction, as radius at left contact decreases.
Thus, the cone will start turning towards left. As it moves, further slipping at $C D$ will start in backward direction which will also turn the cone towards left.
