Rotation 4 Question 8
9. A homogeneous $\operatorname{rod} A B$ of length $L=1.8 m$ and mass $M$ is pivoted at the centre $O$ in such a way that it can rotate freely in the vertical plane (figure).
Show Answer
Answer:
Correct Answer: 9. (a) $\frac{12 v}{7 L}$
(b) $3.5 ms^{-1}$
Solution:
- In this problem we will write $K$ for the angular momentum because $L$ has been used for length of the rod.
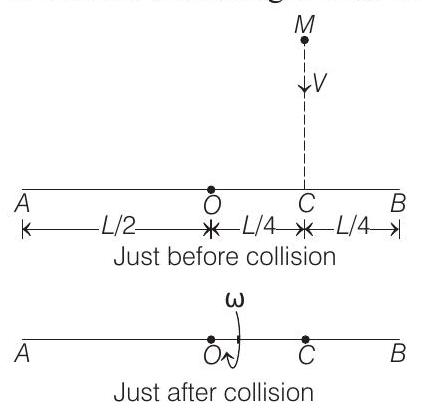
(a) Angular momentum of the system (rod + insect) about the centre of the $\operatorname{rod} O$ will remain conserved just before collision and after collision, i.e. $K _i=K _f$.
$$ \begin{aligned} \text { or } & M v \frac{L}{4} & =I \omega=\frac{M L^{2}}{12}+M \frac{L^{2}}{4} \omega \\ \text { or } & M v \frac{L}{4} & =\frac{7}{48} M L^{2} \omega \\ \text { i.e. } & \omega & =\frac{12}{7} \frac{v}{L} \end{aligned} $$
(b) Due to the torque of weight of insect about $O$, angular momentum of the system will not remain conserved (although angular velocity $\omega$ is constant). As the insect moves towards $B$, moment of inertia of the system increases, hence, the angular momentum of the system will increase.
Let at time $t _1$ the insect be at a distance $x$ from $O$ and by then the rod has rotated through an angle $\theta$. Then, angular momentum at that moment,
$$ \begin{gathered} K=\frac{M L^{2}}{12}+M x^{2} \omega \\ \text { Hence, } \frac{d K}{d t}=2 M \omega x \frac{d x}{d t} \quad(\omega=\text { constant }) \\ \Rightarrow \quad \tau=2 M \omega x \frac{d x}{d t} \Rightarrow M g x \cos \theta=2 M \omega x \frac{d x}{d t} \\ \Rightarrow \quad d x=\frac{g}{2 \omega} \cos \omega t d t \quad \quad(\because \theta=\omega t) \end{gathered} $$
At time $t=0, x=L / 4$ and at time $t=T / 4$ or $\pi / 2 \omega$, $x=L / 2$.
Substituting these limits, we get
$$ \begin{aligned} \int _{L / 4}^{L / 2} d x & =\frac{g}{2 \omega} \int _0^{\pi / 2 \omega}(\cos \omega t) d t \\ {[x] _{L / 4}^{L / 2} } & =\frac{g}{2 \omega^{2}}[\sin \omega t] _0^{\pi / 2 \omega} \\ \Rightarrow \quad \frac{L}{2}-\frac{L}{4} & =\frac{g}{2 \omega^{2}} \sin \frac{\pi}{2}-\sin 0 \\ \frac{L}{4} & =\frac{g}{2 \omega^{2}} \quad \text { or } \quad \omega=\sqrt{\frac{2 g}{L}} \end{aligned} $$
Substituting in Eq. (i), we get
$$ \begin{array}{rlrl} & \sqrt{\frac{2 g}{L}} & =\frac{12}{7} \cdot \frac{v}{L} \\ \text { or } \quad v & =\frac{7}{12} \sqrt{2 g L} \\ & =\frac{7}{12} \sqrt{2 \times 10 \times 1.8} \\ \therefore \quad v & =3.5 m / s \end{array} $$
