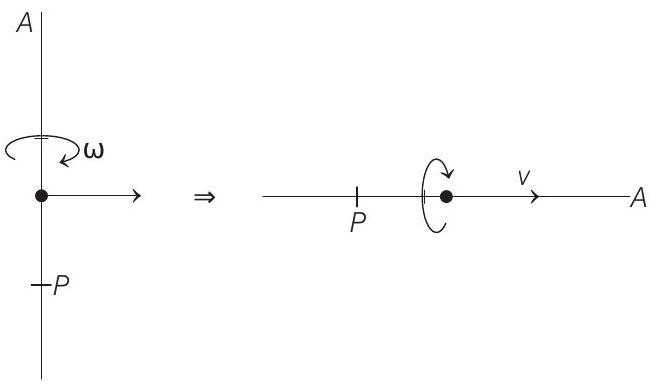
Rotation 4 Question 6
7.
(2000)
(a) Find the ratio
(b) A point
(c) Find the linear speed of the point
Show Answer
Answer:
Correct Answer: 7. (a)
(b)
(c)
Solution:
- (a) Let just after collision, velocity of
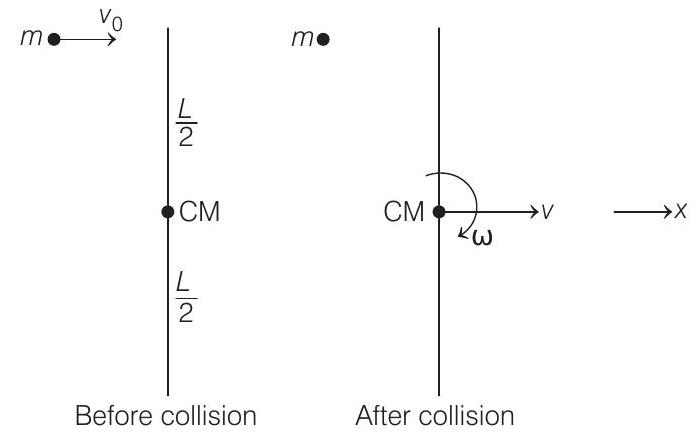
(1) External force on the system (rod + mass) in horizontal plane along
(2) Net torque on the system about CM of rod is zero.
(3) Since, the collision is elastic, kinetic energy is also conserved.
From Eqs. (i), (ii) and (iii), we get the following results
(b) Point
or
or
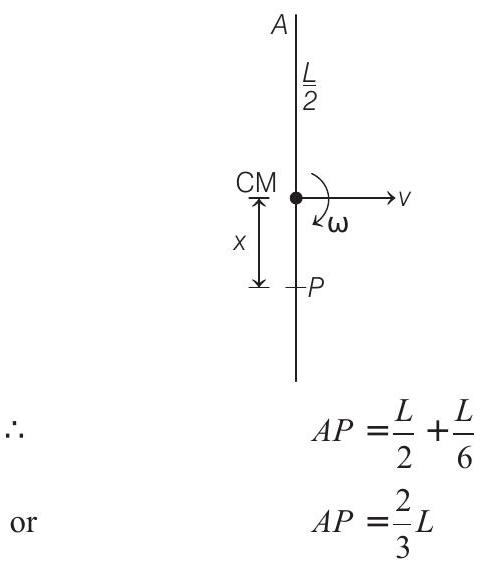
(c) After time
angle rotated by rod,
Therefore, situation will be as shown below