SATHEE: Rotation 4 Question 5

Rotation 4 Question 5

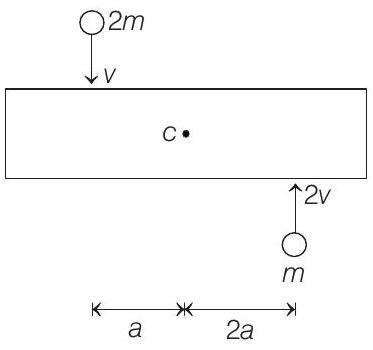6. A uniform bar of length $6 a$ and mass $8 m$ lies on a smooth horizontal table. Two point masses $m$ and $2 m$ moving in the same horizontal plane with speed $2 v$ and $v$ respectively, strike the bar [as shown in the figure] and stick to the bar after collision. Denoting

angular velocity (about the centre of mass), total energy and centre of mass velocity by $ω, E$ and $v_{c}$ respectively, we have after collision

(1991)

(a) $v_{c} = 0$

(b) $ω = \frac{3 v}{5 a}$

(d) $E = \frac{3}{5} m v^{2}$

Analytical Answer Type Questions

Show Answer

Answer:

Correct Answer: 6. (a, c, d)

Solution:

$\begin{aligned} ∴ P_{f} & = 0 or v_{c} = 0 \\ L_{i} & = L_{f} or (2 m v) a + (2 m v) (2 a) = I ω \end{aligned}$

Here, $I = \frac{(8 m) (6 a)^{2}}{12} + m (2 a)^{2} + (2 m) (a^{2}) = 30 m a^{2}$

Substituting in Eq. (i), we get

$ω = \frac{v}{5 a}$

Further, $E = \frac{1}{2} I ω^{2} = \frac{1}{2} \times (30 m a^{2}) {\frac{v}{5 a}}^{2} = \frac{3 m v^{2}}{5}$

पिछला

अगला

Rotation 4 Question 5

6. A uniform bar of length $6 a$ and mass $8 m$ lies on a smooth horizontal table. Two point masses $m$ and $2 m$ moving in the same horizontal plane with speed $2 v$ and $v$ respectively, strike the bar [as shown in the figure] and stick to the bar after collision. Denoting

Analytical Answer Type Questions

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Rotation 4 Question 5

6. A uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving in the same horizontal plane with speed 2v and v respectively, strike the bar [as shown in the figure] and stick to the bar after collision. Denoting

Analytical Answer Type Questions

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu

6. A uniform bar of length $6 a$ and mass $8 m$ lies on a smooth horizontal table. Two point masses $m$ and $2 m$ moving in the same horizontal plane with speed $2 v$ and $v$ respectively, strike the bar [as shown in the figure] and stick to the bar after collision. Denoting