SATHEE: Rotation 4 Question 3

Rotation 4 Question 3

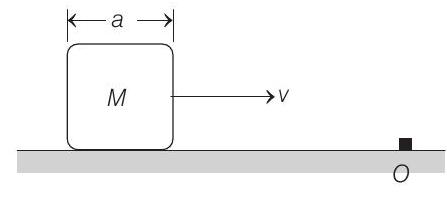
4. A cubical block of side $a$ moving with velocity $v$ on a horizontal smooth plane as shown. It hits a ridge at point $O$ . The angular speed of the block after it hits $O$ is $(1999, 2 M)$

(a) $3 v / 4 a$

(b) $3 v / 2 a$

(d) zero

Objective Questions II (One or more correct option)

Show Answer

Answer:

Correct Answer: 4. (a)

Solution:

$r = \sqrt{2} \frac{a}{2}$ or $r^{2} = \frac{a^{2}}{2}$

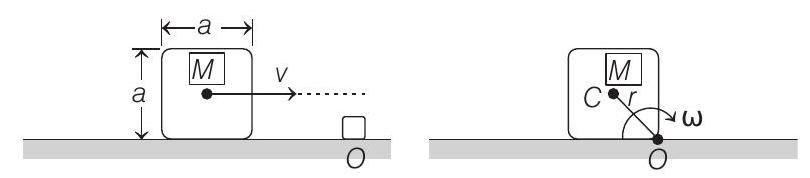
Net torque about $O$ is zero.

Therefore, angular momentum $(L)$ about $O$ will be conserved, or $L_{i} = L_{f}$

$\begin{aligned} M v \frac{a}{2} & = I_{o} ω = (I_{C M} + M r^{2}) ω \\ = \frac{M a^{2}}{6} + M \frac{a^{2}}{2} ω \\ = \frac{2}{3} M a^{2} ω \\ ω & = \frac{3 v}{4 a} \end{aligned}$

पिछला

अगला

Rotation 4 Question 3

4. A cubical block of side $a$ moving with velocity $v$ on a horizontal smooth plane as shown. It hits a ridge at point $O$ . The angular speed of the block after it hits $O$ is $(1999, 2 M)$

Objective Questions II (One or more correct option)

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Rotation 4 Question 3

4. A cubical block of side a moving with velocity v on a horizontal smooth plane as shown. It hits a ridge at point O. The angular speed of the block after it hits O is (1999,2M)

Objective Questions II (One or more correct option)

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu

4. A cubical block of side $a$ moving with velocity $v$ on a horizontal smooth plane as shown. It hits a ridge at point $O$ . The angular speed of the block after it hits $O$ is $(1999, 2 M)$