Rotation 3 Question 8
14. The net external force acting on the disk when its centre of mass is at displacement
(a)
(b)
(c)
(d)
(2008, 4M)
Show Answer
Answer:
Correct Answer: 14. (d)
Solution:
Solving this equation, we get
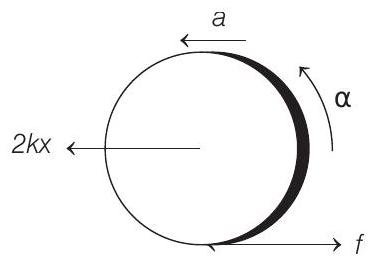
This is opposite to displacement.






