Rotation 3 Question 5
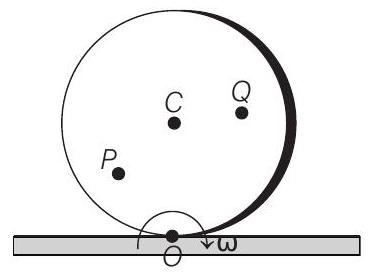
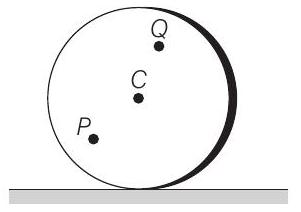
11. A disc is rolling (without slipping) on a horizontal surface.
(2004)
(a)
(b)
(c)
(d) $v _Q
Show Answer
Answer:
Correct Answer: 11. (a)
Solution:
- In case of pure rolling bottom most point is the instantaneous centre of zero velocity.
Velocity of any point on the disc,