SATHEE: Rotation 3 Question 23

Rotation 3 Question 23

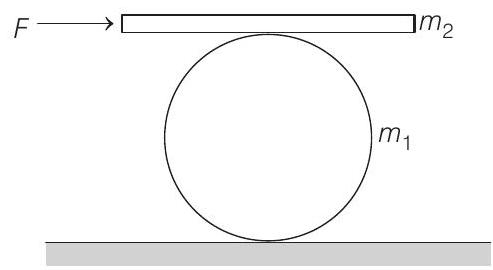
29. A man pushes a cylinder of mass $m_{1}$ with the help of a plank of mass $m_{2}$ as shown. There is no slipping at any contact. The horizontal component of the force applied by the man is $F$ . Find

$(1999, 10 M)$

(a) the accelerations of the plank and the centre of mass of the cylinder and

(b) the magnitudes and directions of frictional forces at contact points.

Show Answer

Solution:

We can choose any arbitrary directions of frictional forces at different contacts.

In the final answer the negative values will show the opposite directions.

Let $f_{1} =$ friction between plank and cylinder

$f_{2} =$ friction between cylinder and ground

$a_{1} =$ acceleration of plank

$a_{2} =$ acceleration of centre of mass of cylinder

and $α =$ angular acceleration of cylinder about its CM.

Since, there is no slipping anywhere

$∴ a_{1} = 2 a_{2}$

$a_{1} = \frac{F - f_{1}}{m_{2}}$

$a_{2} = \frac{f_{1} + f_{2}}{m_{1}}$

$α = \frac{(f_{1} - f_{2}) R}{I} = \frac{(f_{1} - f_{2}) R}{\frac{1}{2} m_{1} R^{2}}$

$α = \frac{2 (f_{1} - f_{2})}{m_{1} R}$

$a_{2} = R α = \frac{2 (f_{1} - f_{2})}{m_{1}}$

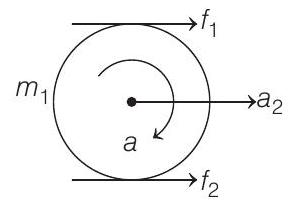
(a) Solving Eqs. (i) to (v), we get

(b)

$\begin{aligned} a_{1} & = \frac{8 F}{3 m_{1} + 8 m_{2}} and a_{2} = \frac{4 F}{3 m_{1} + 8 m_{2}} \\ f_{1} & = \frac{3 m_{1} F}{3 m_{1} + 8 m_{2}}; \\ f_{2} & = \frac{m_{1} F}{3 m_{1} + 8 m_{2}} \end{aligned}$

Since, all quantities are positive, they are correctly shown in figures.

पिछला

अगला

Rotation 3 Question 23

29. A man pushes a cylinder of mass $m_{1}$ with the help of a plank of mass $m_{2}$ as shown. There is no slipping at any contact. The horizontal component of the force applied by the man is $F$ . Find

Solution:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Rotation 3 Question 23

29. A man pushes a cylinder of mass m1 with the help of a plank of mass m2 as shown. There is no slipping at any contact. The horizontal component of the force applied by the man is F. Find

Solution:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu

29. A man pushes a cylinder of mass $m_{1}$ with the help of a plank of mass $m_{2}$ as shown. There is no slipping at any contact. The horizontal component of the force applied by the man is $F$ . Find