Rotation 3 Question 20
26. Two identical uniform discs roll without slipping on two different surfaces
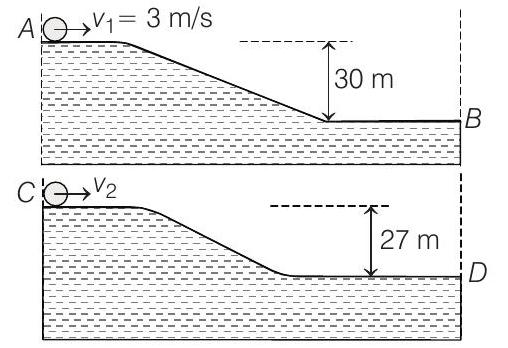
(2015 Adv.)
Show Answer
Answer:
Correct Answer: 26. 7
Solution:
- In case of pure rolling, mechanical energy remains constant (as work-done by friction is zero). Further in case of a disc,
or,
or, Total kinetic energy
Decrease in potential energy =increase in kinetic energy
or,
As final velocity in both cases is same.
So, value of
Solving this equation, we get






