Rotation 3 Question 13
19. The figure shows a system consisting of (i) a ring of outer radius
The ring and disc are separated by frictionless ball bearings. The system is in the
(2012)
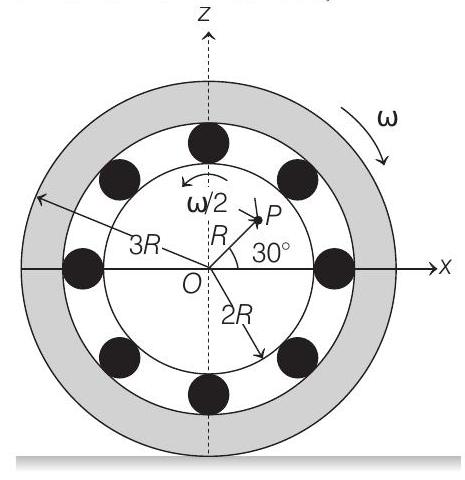
(a) the point
(b) the point
(c) the point
(d) the point
Show Answer
Answer:
Correct Answer: 19.
Solution:
- Velocity of point
In vector form






