Rotation 3 Question 12
18. Two thin circular discs of mass $m$ and $4 m$, having radii of $a$ and $2 a$, respectively, are rigidly fixed by a massless, rigid rod of length $l=\sqrt{24} a$ through their centers. This assembly is laid on a firm and flat surface and set rolling without slipping on the surface so that the angular speed about the axis of the rod is $\omega$. The angular momentum of the entire assembly about the point "
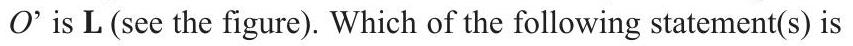(are) true?
(2016 Adv.)
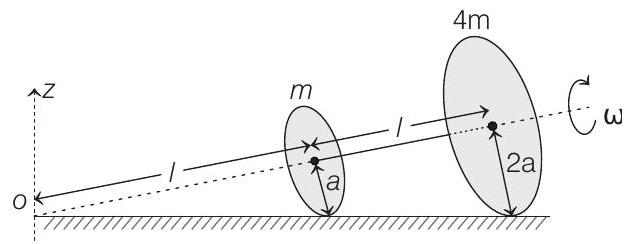
(a) The magnitude of the $z$-component of $\mathbf{L}$ is $55 ma^{2} \boldsymbol{\omega}$
(b) The magnitude of angular momentum of centre of mass of the assembly about the point $O$ is $81 ma^{2} \boldsymbol{\omega}$
(c) The centre of mass of the assembly rotates about the $Z$-axis with an angular speed of $\frac{\omega}{5}$
(d) The magnitude of angular momentum of the assembly about its centre of mass is $17 ma^{2} \frac{\omega}{2}$
Show Answer
Answer:
Correct Answer: 18. (c, d)
Solution:
(a) $\quad L _z=L _{CM-O} \cos \theta-L _{D-CM} \sin \theta$
$$ \begin{aligned} & =\frac{81 \sqrt{24}}{5} a^{2} m \omega \times \frac{\sqrt{24}}{5}-\frac{17 m a^{2} \omega}{2} \times \frac{1}{\sqrt{24}} \\ & =\frac{81 \times 24 m a^{2} \boldsymbol{\omega}}{25}-\frac{17 m a^{2} \omega}{2 \sqrt{24}} \end{aligned} $$
(b) $L _{CM-O}=(5 m) \frac{9 l}{5} \omega \frac{9 l}{5}=\frac{81 m l^{2} \omega}{5}$
$$ \begin{aligned} & =\frac{81 m l^{2}}{5} \times \frac{a \omega}{l} \\ L _{CM-O} & =\frac{81 m l a \omega}{5}=\frac{81 \sqrt{24} a^{2} m \omega}{5} \end{aligned} $$
(c) Velocity of point $P: a \omega=1 \omega$ then $\omega=\frac{a \omega}{1}=$ Angular velocity of C.M. w.r.t.
point $O$.
Angular velocity of CM w.r.t. $Z$-axis $=\omega _0 \cos \theta$
$$ \omega _{CM-z}=\frac{a \omega}{1} \frac{\sqrt{24}}{5}=\frac{a \omega}{\sqrt{24} a} \frac{\sqrt{24}}{5} $$
$$ \begin{aligned} \omega _{CM-z} & =\frac{\omega}{5} \\ \text { (d) } L _{D-CM} & =\frac{m a^{2}}{2} \omega+\frac{4 m(2 a)^{2}}{2} \omega=\frac{17 m a^{2} \omega}{2} \end{aligned} $$
