Rotation 2 Question 9
9. A circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform. Now, the platform is given an angular velocity $\omega _0$. When the tortoise move along a chord of the platform with a constant velocity (with respect to the platform). The angular velocity of the platform $\omega(t)$ will vary with time $t$ as
(2002)
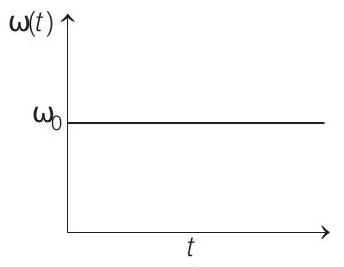
(a)
(c)
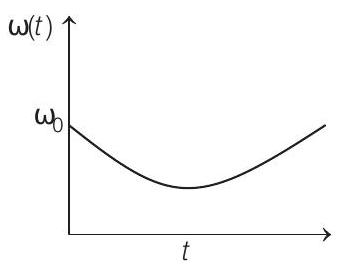
(b)
(d)
Show Answer
Answer:
Correct Answer: 9. (c)
Solution:
- Since, there is no external torque, angular momentum will remain conserved. The moment of inertia will first decrease till the tortoise moves from $A$ to $C$ and then increase as it moves from $C$ and $D$. Therefore, $\omega$ will initially increase and then decrease.
Let $R$ be the radius of platform, $m$ the mass of disc and $M$ is the mass of platform.
Moment of inertia when the tortoise is at $A$
$$ I _1=m R^{2}+\frac{M R^{2}}{2} $$
and moment of inertia when the tortoise is at $B$
$$ \begin{aligned} I _2 & =m r^{2}+\frac{M R^{2}}{2} \\ \text { Here, } \quad r^{2} & =a^{2}+\left[\sqrt{R^{2}-a^{2}}-v t\right]^{2} \end{aligned} $$
From conservation of angular momentum
$$ \omega _0 I _1=\omega(t) I _2 $$
Substituting the values, we can see that variation of $\omega(t)$ is non-linear.
