SATHEE: Rotation 2 Question 15

Rotation 2 Question 15

15. The torque $τ$ on a body about a given point is found to be equal to $A \times L$ , where $A$ is a constant vector and $L$ is the angular momentum of the body about that point. From this it follows that

$(1998, 2$ M)

(a) $\frac{d L}{d t}$ is perpendicular to $L$ at all instants of time

(b) the component of $L$ in the direction of $A$ does not change with time

(d) $L$ does not change with time

Passage Based Questions

Passage 1

A frame of the reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity $ω$ is

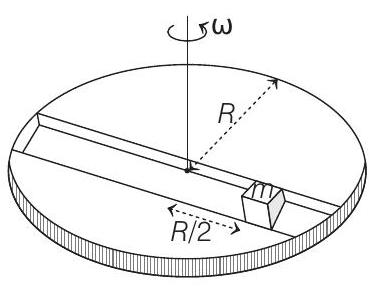an example of a non-inertial frame of reference. The relationship between the force $F_{rot}$ experienced by a particle of mass $m$ moving on the rotating disc and the force $F_{in}$ experienced by the particle in an inertial frame of reference is, $F_{rot} = F_{in} + 2 m (v_{rot} \times \vec{ω}) + m (\vec{ω} \times r) \times \vec{ω}$ , where, $v_{rot}$ is the velocity of the particle in the rotating frame of reference and $r$ is the position vector of the particle with respect to the centre of the disc. Now, consider a smooth slot along a diameter of a disc of radius $R$ rotating counter-clockwise with a constant angular speed $ω$ about its vertical axis through its centre. We assign a coordinate system with the origin at the centre of the disc, the $X$ -axis along the slot, the $Y$ -axis perpendicular to the slot and the $z$ -axis along th rotation axis $(ω = ω k)$ . A small block of mass $m$ is gently placed in the slot at $r = (R / 2) \hat{i}$ at $t = 0$ and is constrained to move only along the slot.

(2016 Adv.)

Show Answer

Answer:

Correct Answer: 15. $(a, b, c)$

Solution:

(a) $τ = A \times L$

i.e. $\frac{d L}{d t} = A \times L$

This relation implies that $\frac{d L}{d t}$ is perpendicular to both $A$ and $L$ .

Differentiating w.r.t. time, we get

$\begin{aligned} \Rightarrow & L \cdot \frac{d L}{d t} + \frac{d L}{d t} \cdot L & = 2 L \frac{d L}{d t} \\ 2 L \cdot \frac{d L}{d t} & = 2 L \frac{d L}{d t} \end{aligned}$

But since,

$L ⊥ \frac{d L}{d t}$

$∴ L \cdot \frac{d L}{d t} = 0$

Therefore, from Eq. (i) $\frac{d L}{d t} = 0$

or magnitude of $L$ i.e. $L$ does not change with time.

(b) So far we are confirm about two points

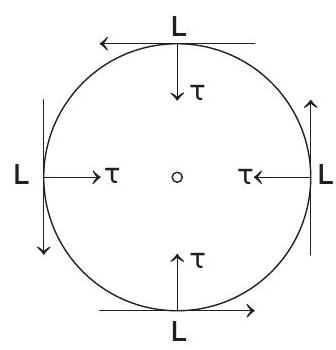
(i) $Tor \frac{d L}{d t} ⊥ L$ and

(ii) $| L | = L$ is not changing with time, therefore, it is a case when direction of $L$ is changing but its magnitude is constant and $τ$ is perpendicular to $L$ at all points.

This can be written as

If $L = (a \cos θ) \hat{i} + (a \sin θ) \hat{j}$

Here, $a =$ positive constant

Then $τ = (a \sin θ) \hat{i} - (a \cos θ) \hat{j}$

So, that $L \cdot τ = 0$ and $L ⊥ τ$

Now, $A$ is constant vector and it is always perpendicular to $τ$ . Thus, $A$ can be written as $A = A \hat{k}$ we can see that $L \cdot A = 0$ i.e. $L ⊥ A$ also.