SATHEE: Rotation 1 Question 7

Rotation 1 Question 7

7. Let the moment of inertia of a hollow cylinder of length 30 $c m$ (inner radius $10 c m$ and outer radius $20 c m$ ) about its axis be $I$ . The radius of a thin cylinder of the same mass such that its moment of inertia about its axis is also $I$ , is

(2019 Main, 12 Jan I)

(a) $16 c m$

(b) $14 c m$

(d) $18 c m$

Show Answer

Answer:

Correct Answer: 7. (a)

Solution:

Moment of inertia of hollow cylinder about its axis is

$I_{1} = \frac{M}{2} (R_{1}^{2} + R_{2}^{2})$

where, $R_{1} =$ inner radius and

$R_{2} =$ outer radius.

Moment of inertia of thin hollow cylinder of radius $R$ about its axis is.

$I_{2} = M R^{2}$

Given, $I_{1} = I_{2}$ and both cylinders have same mass $(M)$ .

So, we have

$\frac{M}{2} (R_{1}^{2} + R_{2}^{2}) = M R^{2}$

$\begin{aligned} (10^{2} + 20^{2}) / 2 = R^{2} \\ R^{2} = 250 = 15.8 \\ R \approx 16 c m \end{aligned}$

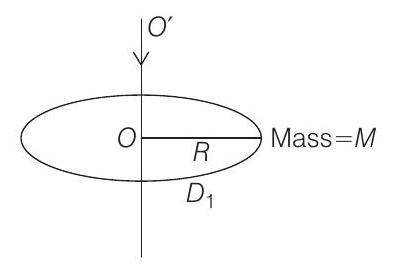
8 For disc $D_{1}$ , moment of inertia across axis $O O^{'}$ will be

$I_{1} = \frac{1}{2} M R^{2}$

For discs $D_{2}$ and $D_{3}, O O^{'}$ is an axis parallel to the diameter of disc. Using parallel axis theorem,

$I_{2} = I_{3} = I_{diameter} + M d^{2}$

$\begin{aligned} Here, I_{diameter} = \frac{1}{4} M R^{2} \\ and d = R \\ ∴ I_{2} = I_{3} = \frac{1}{4} M R^{2} + M R^{2} = \frac{5}{4} M R^{2} \end{aligned}$

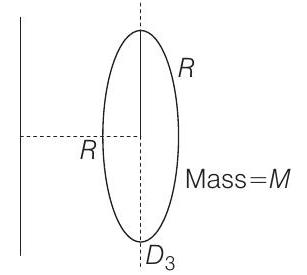
Now, total MI of the system

$I = I_{1} + I_{2} + I_{3} = \frac{1}{2} M R^{2} + 2 \times \frac{5}{4} M R^{2} = 3 M R^{2}$

9 (b) Suppose the mass of the $△ A B C$ be ’ $M$ ’ and length of the side be ’ $l$ ‘.

When the $△ D E F$ is being removed from it, then the mass of the removed $Δ$ will be ’ $M / 4$ ’ and length of its side will be ’ $l / 2$ ’ as shown below

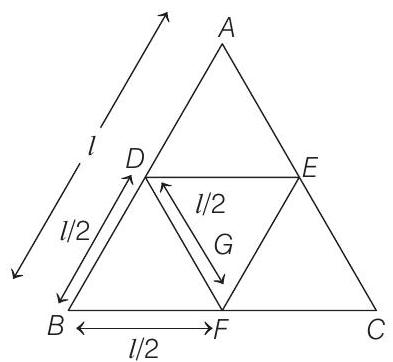
Since we know, moment of inertia of the triangle about the axis, passing through its centre of gravity is, $I = k m l^{2}$ , where $k$ is a constant. Then for $△ D E F$ , moment of inertia of the triangle about the axis,

$I = k \frac{M}{4} {\frac{l}{2}}^{2} = \frac{k M l^{2}}{16}$

Moment of inertia of $△ A B C$ is

$I_{0} = k M l^{2}$

The moment of inertia of the remaining part will be

$\begin{aligned} I^{'} = I_{0} - I & = k M l^{2} - \frac{k M l^{2}}{16} [∵ using Eqs. (i) and (ii)] \\ = \frac{15 k M l^{2}}{16} or I^{'} = \frac{15}{16} I_{0} \end{aligned}$

Key Idea This problem will be solved by applying parallel axis theorem, which states that moment of inertia of a rigid body about any axis is equals to its moment of inertia about a paralle axis through its centre of mass plus the product of the mass of the body and the square of the perpendicular distance between the axis.

We know that moment of inertia (MI) about the principle axis of the sphere is given by

$I_{sphere} = \frac{2}{5} M R^{2}$

Using parallel axis theorem, moment of inertia about the given axis in the figure below will be

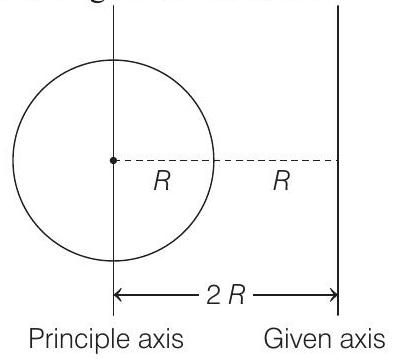
$\begin{aligned} I_{1} = \frac{2}{5} M R^{2} + M (2 R)^{2} \\ I_{1} = \frac{22}{5} M R^{2} \end{aligned}$

Considering both spheres at equal distance from the axis, moment of inertia due to both spheres about this axis will be

$2 I_{1} = 2 \times 22 / 5 M R^{2}$

Now, moment of inertia of rod about its perpendicular bisector axis is given by

$I_{2} = \frac{1}{12} M L^{2}$

Here, given that

$L = 2 R$

$∴ I_{2} = \frac{1}{12} M (2 R)^{2} = \frac{1}{3} M R^{2}$

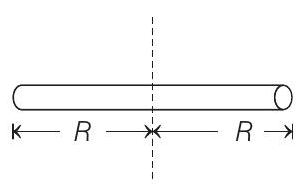
So, total moment of inertia of the system is

$\begin{aligned} I = 2 I_{1} + I_{2} = 2 \times \frac{22}{5} M R^{2} + \frac{1}{3} M R^{2} \\ \Rightarrow I & = \frac{44}{5} + \frac{1}{3} M R^{2} = \frac{137}{15} M R^{2} \end{aligned}$