Rotation 1 Question 5
5. A thin circular plate of mass
(a)
(b)
(c)
(d)
(2019 Main, 8 April I)
Show Answer
Answer:
Correct Answer: 5. (*)
Solution:
- Consider an elementary ring of thickness
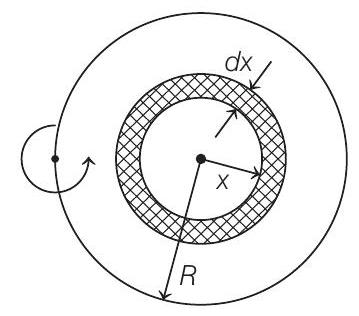
Moment of inertia of this ring about a perpendicular axes through centre is
Moment of inertia of this elementary ring about a perpendicular axes at a point through edge, (by parallel axes theorem)
Moment of inertia of complete disc is






