Rotation 1 Question 2
2. A solid sphere of mass
The ratio
(2019 Main, 10 Apri II)
(a) 285
(b) 185
(c) 65
(d) 140
Show Answer
Answer:
Correct Answer: 2. (d)
Solution:
- The given situation is shown in the figure given below
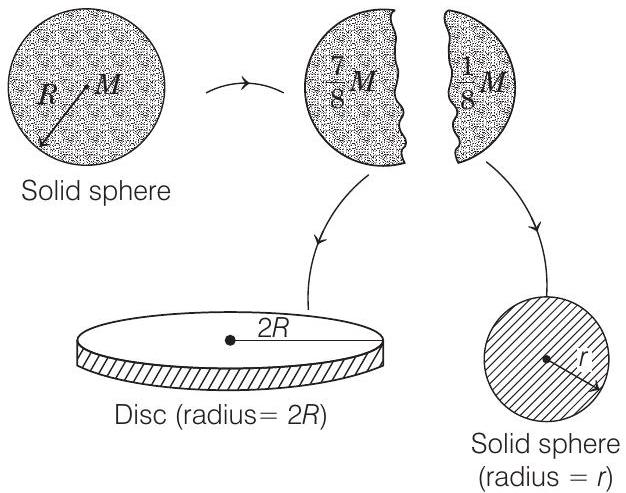
Density of given sphere of radius
Let radius of sphere formed from second part is
Now,
and






