Rotation 1 Question 19
22. A lamina is made by removing a small disc of diameter
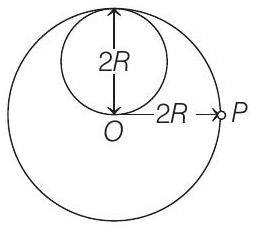
(2012)
Show Answer
Answer:
Correct Answer: 22. (3)
Solution:
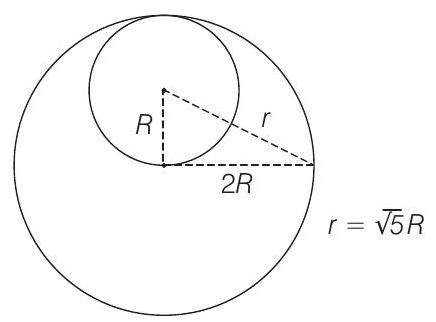
Then,
For
For
Therefore, the nearest integer is 3 .






