Rotation 1 Question 18
21. The moment of inertia of a thin square plate
(a)
(b)
(c)
(d)
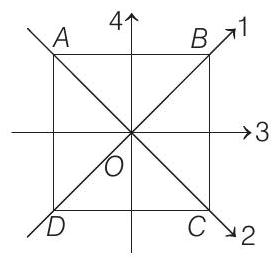
where,
Integer Answer Type Questions
Show Answer
Answer:
Correct Answer: 21. (a, b, c)
Solution:
- Since, it is a square lamina
(by symmetry)
From perpendicular axes theorem,
Moment of inertia about an axis perpendicular to square plate and passing from
or
Rather we can say
Therefore,






