Rotation 1 Question 14
17. From a circular disc of radius
(2005)
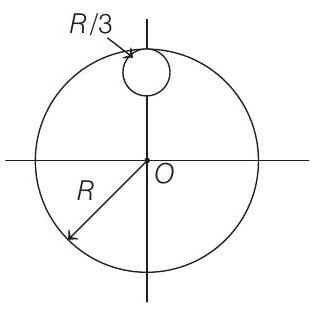
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 17. (a)
Solution:
or
Here,
Substituting in Eq. (i), we have






