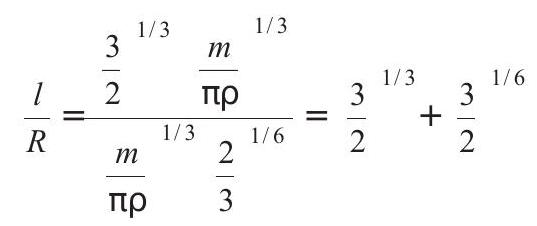Rotation 1 Question 10
13. The moment of inertia of a uniform cylinder of length
(a)
(b) 1
(c)
(d)
(2017 Main)
Show Answer
Answer:
Correct Answer: 13. (d)
Solution:
- MI of a solid cylinder about its perpendicular bisector of length is
For