Rotation 1 Question 1
1. A circular disc of radius $b$ has a hole of radius $a$ at its centre (see figure). If the mass per unit area of the disc varies as $\frac{\sigma _0}{r}$, then the radius of gyration of the
disc about its axis passing through the centre is (2019 Main, 12 April I)
(a) $\sqrt{\frac{a^{2}+b^{2}+a b}{2}}$
(b) $\frac{a+b}{2}$
(c) $\sqrt{\frac{a^{2}+b^{2}+a b}{3}}$
(d) $\frac{a+b}{3}$
Show Answer
Answer:
Correct Answer: 1. (c)
Solution:
- Key Idea Radius of gyration $K$ of any structure is given by
$$ I=M K^{2} \text { or } K=\sqrt{\frac{I}{M}} $$
To find $K$, we need to find both moment of inertia I and mass $M$ of the given structure.
Given, variation in mass per unit area (surface mass density),
$$ \sigma=\frac{\sigma _0}{r} $$
Calculation of Mass of Disc
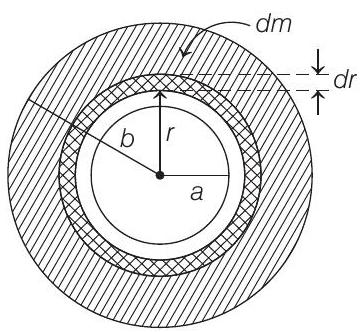
Let us divide whole disc in small area elements, one of them shown at $r$ distance from the centre of the disc with its width as $d r$.
Mass of this element is
$$ \begin{aligned} d m & =\sigma \cdot d A \\ \Rightarrow \quad d m & =\frac{\sigma _0}{r} \times 2 \pi r d r \quad \text { [from Eq. (i)] } \end{aligned} $$
Mass of the disc can be calculated by integrating it over the given limits of $r$,
$$ \begin{aligned} \quad \int _0^{M} d m & =\int _a^{b} \sigma _0 \times 2 \pi \times d r \\ M & =\sigma _0 2 \pi(b-a) \end{aligned} $$
Calculation of Moment of Inertia
$$ \begin{aligned} I=\int _0^{M} r^{2} d m & =\int _a^{b} r^{2} \cdot \frac{\sigma _0}{r} \times 2 \pi r d r=\sigma _0 2 \pi \int _a^{b} r^{2} d r=\sigma _0 2 \pi \frac{r}{3} _a^{b} \\ \Rightarrow \quad I & =\frac{1}{3} \sigma _0 2 \pi\left[b^{3}-a^{3}\right] \end{aligned} $$
Now, radius of gyration,
$$ \begin{aligned} K & =\sqrt{\frac{I}{M}}=\sqrt{\frac{\frac{2 \pi \sigma _0}{3}\left(b^{3}-a^{3}\right)}{2 \pi \sigma _0(b-a)}} \\ \Rightarrow \quad K & =\sqrt{\frac{1}{3} \frac{\left(b^{3}-a^{3}\right)}{b-a}} \end{aligned} $$
As we know, $b^{3}-a^{3}=(b-a)\left(b^{2}+a^{2}+a b\right)$
$$ \begin{array}{rlrl} & \therefore & K & =\sqrt{\frac{1}{3}\left(b^{2}+a^{2}+a b\right)} \\ \text { or } & K & =\sqrt{\frac{\left(a^{2}+b^{2}+a b\right)}{3}} \end{array} $$
