Properties of Matter 4 Question 12
14. Two spheres
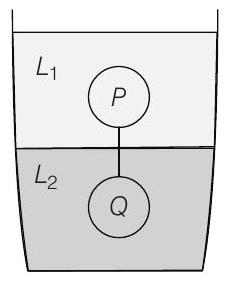and the string being taut (see figure). If sphere
(2015 Adv.)
(a)
(b)
(c)
(d)
Assertion and Reason
Mark your answer as
(a) If Statement I is true, Statement II is true; Statement II is the correct explanation for Statement I
(b) If Statement I is true, Statement II is true; Statement II is not a correct explanation for Statement I
(c) If Statement I is true; Statement II is false
(d) If Statement I is false; Statement II is true
Show Answer
Answer:
Correct Answer: 14. 3
Solution:
- Terminal velocity is given by
