Properties of Matter 3 Question 1
7. A glass tube of uniform internal radius
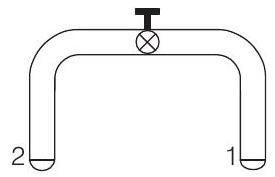 has a hemispherial soap bubble of radius
has a hemispherial soap bubble of radius
Just after opening the valve.
(2008, 3M)
(a) air from end 1 flows towards end 2. No change in the volume of the soap bubbles
(b) air from end 1 flows towards end 2. Volume of the soap bubble at end 1 decreases
(c) no change occurs
(d) air from end 2 flows towards end 1. Volume of the soap bubble at end 1 increases
Show Answer
Answer:
Correct Answer: 7. (a)
Solution:
- Applying continuity equation at 1 and 2 , we have
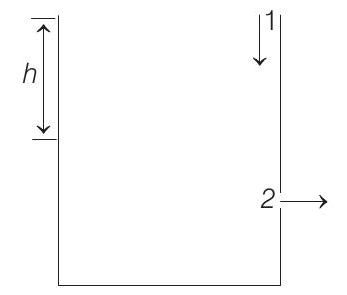
Further applying Bernoulli’s equation at these two points, we have
Solving Eqs. (i) and (ii), we have
Substituting the values, we have






