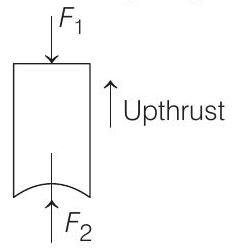
Properties of Matter 2 Question 5
5. A hemispherical portion of radius
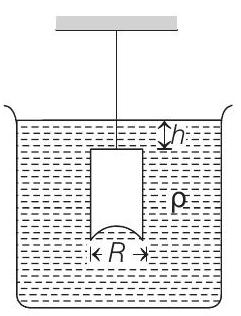
upper surface of the cylinder is at a depth
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 5. (a)
Solution: