Properties of Matter 2 Question 23
23. A column of mercury of length $10 cm$ is contained in the middle of a horizontal tube of length $1 m$ which is closed at both the ends. The two equal lengths contain air at standard atmospheric pressure of $0.76 m$ of mercury. The tube is now turned to vertical position. By what distance will the column of mercury be displaced? Assume temperature to be constant.
(1978)
momentum and, $25 %$ comes back with the same speed. The resultant pressure on the mesh will be (2019 Main, 11 Jan I)
(a) $\rho v^{2}$
(b) $\frac{1}{2} \rho v^{2}$
(c) $\frac{1}{4} \rho v^{2}$
(d) $\frac{3}{4} \rho v^{2}$
5 Water flows into a large tank with flat bottom at the rate of $10^{-4} m^{3} s^{-1}$. Water is also leaking out of a hole of area $1 cm^{2}$ at its bottom. If the height of the water in the tank remains steady, then this height is
(2019 Main, 10 Jan I)
(a) $4 cm$
(b) $2.9 cm$
(c) $5.1 cm$
(d) $1.7 cm$
6 The top of a water tank is open to air and its water level is maintained. It is giving out $0.74 m^{3}$ water per minute through a circular opening of $2 cm$ radius is its wall. The depth of the centre of the opening from the level of water in the tank is close to
(2019 Main, 9 Jan II)
(a) $4.8 m$
(b) $6.0 m$
(c) $2.9 m$
(d) $9.6 m$
Show Answer
Solution:
- Let area of cross-section of the tube be $A$.
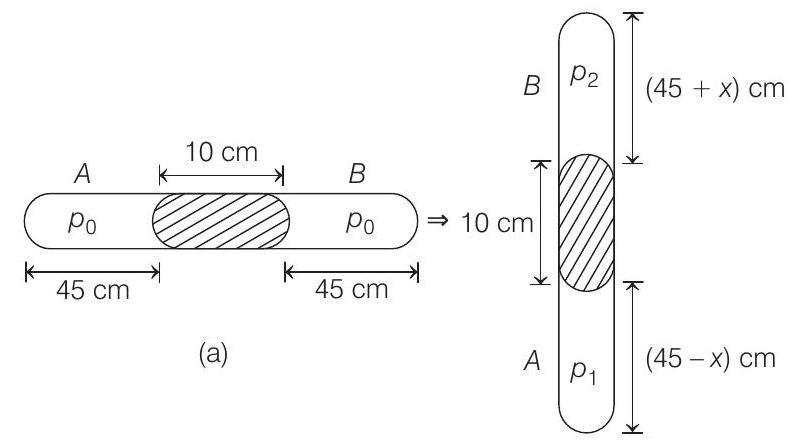
(b)
Applying $p _1 V _1=p _2 V _2$ in $A$ and $B$ we have,
$$ \begin{aligned} & p _0(45)(A) & =p _1(45-x) A \\ & \text { or } \quad 76 \times 45 & =p _1(45-x) \\ & p _0(45)(A) & =p _2(45+x) A \\ & 76 \times 45 & =p _2(45+x) \end{aligned} $$
From Eqs. (i) and (ii), we get
$$ \left(p _1-p _2\right)=76 \times 45\left(\frac{1}{45-x}-\frac{1}{45+x}\right) $$
From figure (b),
$\left(p _1-p _2\right) A=$ Weight of $10 cm$ of Hg column
or $\quad p _1-p _2=$ Pressure equivalent to $10 cm$ of $Hg$ column
$$ 76 \times 45\left(\frac{1}{45-x}-\frac{1}{45+x}\right)=10 $$
Solving this equation, we get
$$ x=2.95 cm $$
