Properties of Matter 2 Question 19
19. A uniform solid cylinder of density $0.8 g / cm^{3}$ floats in equilibrium in a combination of two non-mixing liquids $A$ and $B$ with its axis vertical. The densities of the liquids $A$ and $B$ are $0.7 g / cm^{3}$ and $1.2 g / cm^{3}$, respectively. The height of liquid $A$ is $h _A=1.2 cm$. The length of the part of the cylinder immersed in liquid $B$ is $h _B=0.8 cm$.
(2002, 5M)
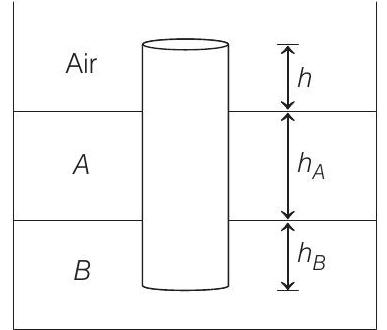
(a) Find the total force exerted by liquid $A$ on the cylinder.
(b) Find $h$, the length of the part of the cylinder in air.
(c) The cylinder is depressed in such a way that its top surface is just below the upper surface of liquid $A$ and is then released. Find the acceleration of the cylinder immediately after it is released.
Show Answer
Answer:
Correct Answer: 19. $\pi R^{2} L(\sqrt{\rho \sigma}-\rho)$
Solution:
- (a) Liquid $A$ is applying the hydrostatic force on cylinder from all the sides. So, net force is zero.
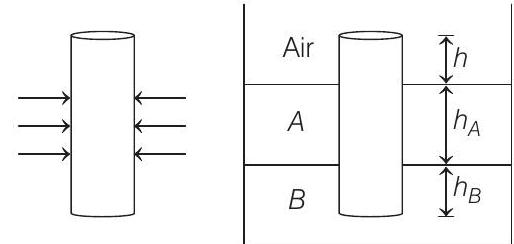
(b) In equilibrium
Weight of cylinder $=$ Net upthrust on the cylinder
Let $s$ be the area of cross-section of the cylinder, then weight $=(s)\left(h+h _A+h _B\right) \rho _{\text {cylinder }} g$
and upthrust on the cylinder
= upthrust due to liquid $A+$ upthrust due to liquid $B$
$=s h _A \rho _A g+s h _B \rho _B g$
Equating these two,
$s\left(h+h _A+h _B\right) \rho _{\text {cylinder }} g=s g\left(h _A \rho _A+h _B \rho _B\right)$
or $\left(h+h _A+h _B\right) \rho _{\text {cylinder }}=h _A \rho _A+h _B \rho _B$
Substituting,
$h _A=1.2 cm, h _B=0.8 cm$ and $\rho _A=0.7 g / cm^{3}$
$\rho _B=1.2 g / cm^{3}$ and $\rho _{\text {cylinder }}=0.8 g / cm^{3}$
In the above equation, we get $h=0.25 cm$
(c) Net upward force $=$ extra upthrust $=\operatorname{sh} \rho _B g$
$\therefore$ Net acceleration $a=\frac{\text { Force }}{\text { Mass of cylinder }}$
$$ \begin{aligned} \text { or } & a=\frac{s h \rho _B g}{s\left(h+h _A+h _B\right) \rho _{\text {cylinder }}} \\ \text { or } & a=\frac{h \rho _B g}{\left(h+h _A+h _B\right) \rho _{\text {cylinder }}} \end{aligned} $$
Substituting the values of $h, h _A h _B, \rho _B$ and $\rho _{\text {cylinder }}$, we get, $a=\frac{g}{6}$
(upwards)
