Properties of Matter 2 Question 1
1. A submarine experience a pressure of
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 1. (d)
Solution:
- Pressure inside a fluid volume open to atmosphere is
where,
and
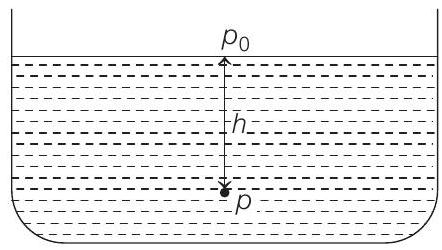
In problem given,
when
So, we have
Given,
and






