Properties of Matter 1 Question 6
6. A load of mass $M kg$ is suspended from a steel wire of length $2 m$ and radius $1.0 mm$ in Searle’s apparatus experiment. The increase in length produced in the wire is $4.0 mm$. Now, the load is fully immersed in a liquid of relative density 2 . The relative density of the material of load is 8 . The new value of increase in length of the steel wire is
(2019 Main, 12 Jan II)
(a) zero
(b) $5.0 mm$
(c) $4.0 mm$
(d) $3.0 mm$
Show Answer
Answer:
Correct Answer: 6. (d)
Solution:
- When load $M$ is attached to wire, extension in length of wire is
$$ \Delta l _1=\frac{M g l}{A . Y} $$
where, $Y$ is the Young’s modulus of the wire.
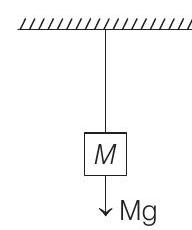
when load is immersed in liquid of relative density 2, increase in length of wire as shown in the figure is
$$ \Delta l _2=\frac{\left(M g-F _B\right) l}{A . Y} $$
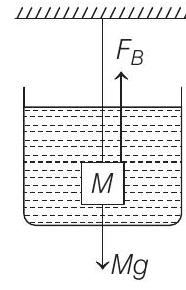
where, $F _B=$ Buoyant force
$\therefore \quad \Delta l _2=\frac{\left(M g-M g \cdot \frac{\rho _l}{\rho _b}\right) l}{A . Y} \quad\left[\because F _B=V \rho _l g=\frac{M g}{\rho _b} \rho _l g\right]$
Here given that, $\frac{\rho _l}{\rho _b}=\frac{2}{8}=\frac{1}{4}$
So, $\quad \Delta l _2=\frac{\left(\frac{3}{4} M g\right) l}{A . Y}$
Dividing Eqs. (ii) by (i), we get
$$ \Rightarrow \begin{aligned} \frac{\Delta l _2}{\Delta l _1} & =\frac{3}{4} \\ \Delta l _2 & =\frac{3}{4} \times \Delta l _1 \\ & =\frac{3}{4} \times 4 mm=3 mm \end{aligned} $$
