Properties of Matter 1 Question 12
12. The adjacent graph shows the extension $(\Delta l)$ of a wire of length $1 m$ suspended from the top of a roof at one end and with a load $w$ connected to the other end. If the cross-sectional area of the wire is $10^{-6} m^{2}$, calculate from the graph the Young’s modulus of the material of the wire.
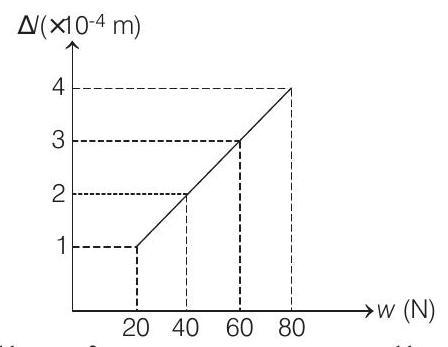
(2003, 2M)
(a) $2 \times 10^{11} N / m^{2}$
(b) $2 \times 10^{-11} N / m^{2}$
(c) $3 \times 10^{12} N / m^{2}$
(d) $2 \times 10^{13} N / m^{2}$
Show Answer
Answer:
Correct Answer: 12. (a)
Solution:
- $\Delta l=\left(\frac{l}{Y A}\right) \cdot w$
i.e. graph is a straight line passing through origin (as shown in question also), the slope of which is $\frac{l}{Y A}$.
$$ \begin{array}{rlrl} \therefore \quad & \text { Slope } & =\left(\frac{l}{Y A}\right) \\ \therefore \quad & Y & =\left(\frac{l}{A}\right)\left(\frac{1}{\text { slope }}\right)=\left(\frac{1.0}{10^{-6}}\right) \frac{(80-20)}{(4-1) \times 10^{-4}} \\ & =2.0 \times 10^{11} N / m^{2} \end{array} $$
