Properties of Matter 1 Question 1
1. In an experiment, brass and steel wires of length $1 m$ each with areas of cross-section $1 mm^{2}$ are used. The wires are connected in series and one end of the combined wire is connected to a rigid support and other end is subjected to elongation. The stress requires to produce a net elongation of $0.2 mm$ is
[Take, the Young’s modulus for steel and brass are respectively $120 \times 10^{9} N / m^{2}$ and $60 \times 10^{9} N / m^{2}$ ]
(2019 Main, 10 April II)
(a) $1.2 \times 10^{6} N / m^{2}$
(b) $0.2 \times 10^{6} N / m^{2}$
(c) $1.8 \times 10^{6} N / m^{2}$
(d) $4.0 \times 10^{6} N / m^{2}$
Show Answer
Answer:
Correct Answer: 1. (*)
Solution:
- In given experiment, a composite wire is stretched by a force $F$.
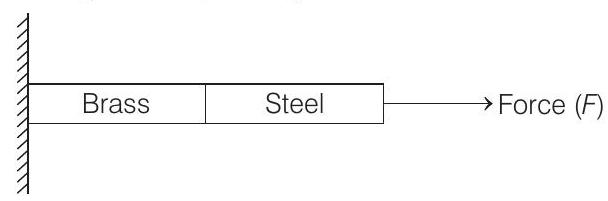
Net elongation in the wire $=$ elongation in brass wire + elongation in steel wire
Now, Young’s modulus of a wire of cross-section $(A)$ when some force $(F)$ is applied, $Y=\frac{F l}{A \Delta l}$
We have,
$$ \Delta l=\text { elongation }=\frac{F l}{A Y} $$
So, from relation (i), we have
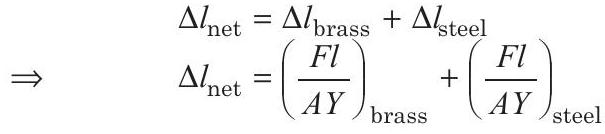
As wires are connected in series and they are of same area of cross-section, length and subjected to same force, so
$$ \Delta l _{\text {net }}=\frac{F}{A}\left(\frac{l}{Y _{\text {brass }}}+\frac{l}{Y _{\text {steel }}}\right) $$
Here,
$$ \begin{aligned} & \qquad \Delta l _{\text {net }}=0.2 mm=0.2 \times 10^{-3} m \\ & \text { and } \begin{array}{l} l=1 m \\ Y _{\text {brass }}=60 \times 10^{9} Nm^{-2}, Y _{\text {steel }}=120 \times 10^{9} Nm^{-2} \end{array} \end{aligned} $$
On putting the values, we have
$$
