Optics 7 Question 5
5. Consider a tank made of glass (refractive index is 1.5 ) with a thick bottom. It is filled with a liquid of refractive index
For this to happen, the minimum value of
(2019 Main, 9 Jan I)
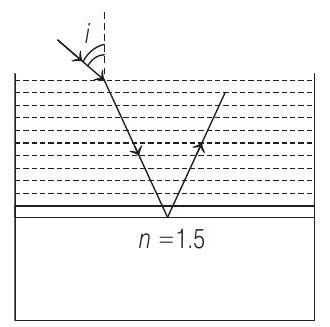
(a)
(b)
(c)
(d)
Show Answer
Solution:
Key Idea When a beam of unpolarised light is reflected from a transparent medium of refractive index
In the given condition, the light reflected irrespective of an angle of incidence is never completely polarised. So,
where,
From Brewster’s law, we know that
From Eqs. (i) and (ii), we get






