SATHEE: Optics 7 Question 44

Optics 7 Question 44

45. Monochromatic light is incident on a plane interface $A B$ between two media of refractive indices $n_{1}$ and $n_{2} (n_{2} > n_{1})$ at an angle of incidence $θ$ as shown in the figure.

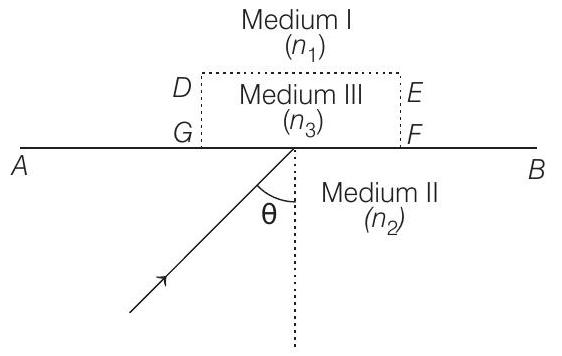
The angle $θ$ is infinitesimally greater than the critical angle for the two media so that total internal reflection takes place. Now if a transparent slab DEFG of uniform thickness and of refractive index $n_{3}$ is introduced on the interface (as shown in the figure), show that for any value of $n_{3}$ all light will ultimately be reflected back again into medium II.

Consider separately the cases :

(1986, 6M)

(a) $n_{3} < n_{1}$ and

(b) $n_{3} > n_{1}$

Show Answer

Answer:

Correct Answer: 45. $13.97 W / m^{2}$

Solution:

Given $θ$ is slightly greater than $\sin^{- 1} \frac{n_{1}}{n_{2}}$

(a) When $n_{3} < n_{1}$

$\begin{aligned} i.e. n_{3} < n_{1} < n_{2} \\ or \frac{n_{3}}{n_{2}} < \frac{n_{1}}{n_{2}} or \sin^{- 1} \frac{n_{3}}{n_{2}} < \sin^{- 1} \frac{n_{1}}{n_{2}} \end{aligned}$

Hence, critical angle for III and II will be less than the critical angle for II and I. So, if TIR is taking place between I and II, then TIR will definitely take place between I and III.

(b) When $n_{3} > n_{1}$ Now two cases may arise :

Case $1 n_{1} < n_{3} < n_{2}$

In this case there will be no TIR between II and III but TIR will take place between III and I. This is because

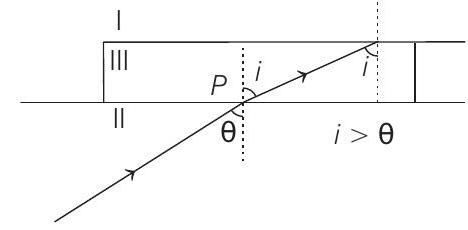
Ray of light first enters from II to III $i e$ , from denser to rarer.

$∴ i > θ$

Applying Snell’s law at $P$

$n_{2} \sin θ = n_{3} \sin i or \sin i = \frac{n_{2}}{n_{3}} \sin θ$

Since, $\sin θ$ is slightly greater than $\frac{n_{1}}{n_{2}}$

$∴ \sin i$ is slightly greater than $\frac{n_{2}}{n_{3}} \times \frac{n_{1}}{n_{2}}$ or $\frac{n_{1}}{n_{3}}$

but $\frac{n_{1}}{n_{3}}$ is nothing but $\sin {(θ_{c})}_{I, I I I}$

$∴ \sin (i)$ is slightly greater than $\sin {(θ_{c})}_{I, I I I}$

Or TIR will now take place on I and III and the ray will be reflected back.

Case $2 n_{1} < n_{2} < n_{3}$

This time while moving from II to III, ray of light will bend towards normal. Again applying Snell’s law at $P$

$\begin{aligned} n_{2} \sin θ & = n_{3} \sin i \\ \Rightarrow \sin i & = \frac{n_{2}}{n_{3}} \sin θ \end{aligned}$

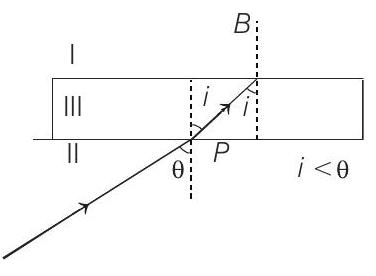
Since, $\sin θ$ slightly greater than $\frac{n_{1}}{n_{2}}$ $\sin i$ will be slightly greater than $\frac{n_{2}}{n_{3}} \times \frac{n_{1}}{n_{2}}$ or $\frac{n_{1}}{n_{3}}$

but $\frac{n_{1}}{n_{3}}$ is $\sin {(θ_{c})}_{I, III}$

i.e. $\sin i > \sin {(θ_{c})}_{I, III}$ or $i > {(θ_{c})}_{I, I I I}$

Therefore, TIR will again take place between I and III and the ray will be reflected back.

NOTE Case I and case 2 of $n_{3} > n_{1}$ can be explained by one equation only. But two cases are deliberately formed for better understanding of refraction, Snell’s law and total internal reflection (TIR).