SATHEE: Optics 7 Question 40

Optics 7 Question 40

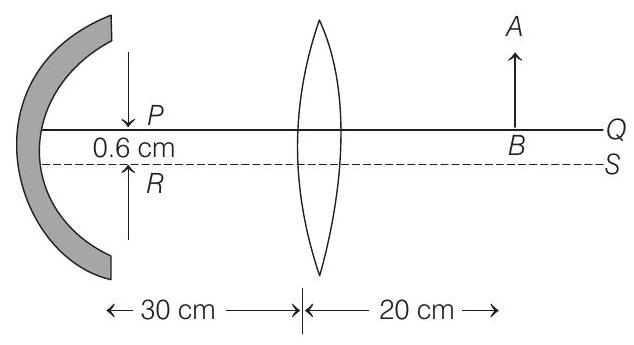
41. A convex lens of focal length $15 c m$ and a concave mirror of focal length $30 c m$ are kept with their optic axis $P Q$ and $R S$ parallel but separated in vertical direction by $0.6 c m$ as shown.

The distance between the lens and mirror is $30 c m$ . An upright object $A B$ of height $1.2 c m$ is placed on the optic axis $P Q$ of the lens at a distance of $20 c m$ from the lens. If $A^{'} B^{'}$ is the image after refraction from the lens and the reflection from the mirror, find the distance of $A^{'} B^{'}$ from the pole of the mirror and obtain its magnification. Also locate positions of $A^{'}$ and $B^{'}$ with respect to the optic axis $R S$ .

$(2000, 6 M)$

Show Answer

Answer:

Correct Answer: 41. $15 c m, - 3 / 2$

Solution:

(a) Rays coming from object $A B$ first refract from the lens and then reflect from the mirror.

Refraction from the lens

$u = - 20 c m, f = + 15 c m$

Using lens formula $\frac{1}{v} - \frac{1}{u} = \frac{1}{f} \Rightarrow \frac{1}{v} - \frac{1}{- 20} = \frac{1}{15}$

$∴ v = + 60 c m$

and linear magnification, $m_{1} = \frac{v}{u} = \frac{+ 60}{- 20} = - 3$

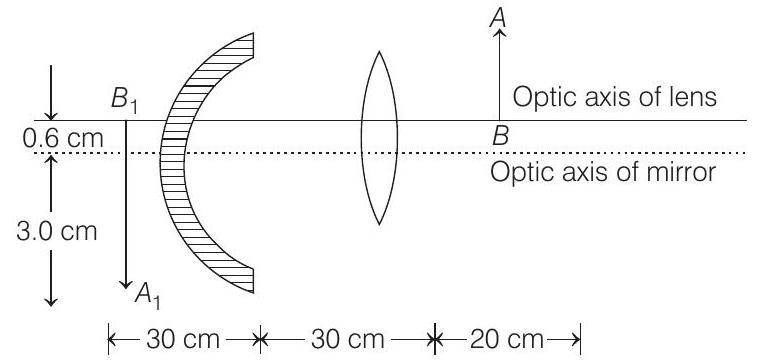
i.e. first image formed by the lens will be at $60 c m$ from it (or $30 c m$ from mirror) towards left and 3 times magnified but inverted. Length of first image $A_{1} B_{1}$ would be $1.2 \times 3 = 3.6 c m$ (inverted).

Reflection from mirror Image formed by lens $(A_{1} B_{1})$ will behave like a virtual object for mirror at a distance of $30 c m$ from it as shown. Therefore $u = + 30 c m$ , $f = - 30 c m$ .

Using mirror formula, $\frac{1}{v} + \frac{1}{u} = \frac{1}{f}$ or $\frac{1}{v} + \frac{1}{30} = - \frac{1}{30}$

$∴ v = - 15 c m$

and linear magnification,

$m_{2} = - \frac{v}{u} = - \frac{- 15}{+ 30} = + \frac{1}{2}$

i.e. final image $A^{'} B^{'}$ will be located at a distance of $15 c m$ from the mirror (towards right) and since magnification is $+ \frac{1}{2}$ , length of final image would be $3.6 \times \frac{1}{2} = 1.8 c m$ .

$∴ A^{'} B^{'} = 1.8 c m$

Point $B_{1}$ is $0.6 c m$ above the optic axis of mirror, therefore, its image $B^{'}$ would be (0.6) $\frac{1}{2} = 0.3 c m$ above optic axis. Similarly, point $A_{1}$ is $3 c m$ below the optic axis, therefore, its image $A^{'}$ will be $3 \times \frac{1}{2} = 1.5 c m$ below the optic axis as shown below

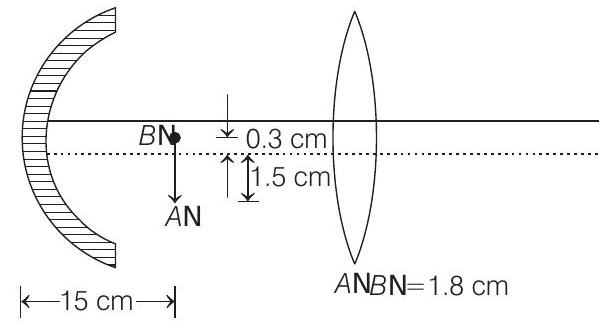
Total magnification of the image,

$\begin{matrix} m = m_{1} \times m_{2} = (- 3) + \frac{1}{2} = - \frac{3}{2} \\ ∴ A^{'} B^{'} = (m) (A B) = - \frac{3}{2} (1.2) = - 1.8 c m \end{matrix}$

Note that, there is no need of drawing the ray diagram if not asked in the question.

NOTE With reference to the pole of an optical instrument (whether it is a lens or a mirror) the coordinates of the object $(X_{0}, Y_{0})$ are generally known to us. The corresponding coordinates of image $(X_{i}, Y_{i})$ are found as follows