Optics 7 Question 4
4. The eye can be regarded as a single refracting surface. The radius of curvature of this surface is equal to that of cornea $(7.8 mm)$. This surface separates two media of refractive indices 1 and 1.34. Calculate the distance from the refracting surface at which a parallel beam of light will come to focus.
(2019 Main, 10 Jan II)
(a) $4.0 cm$
(b) $2 cm$
(c) $3.1 cm$
(d) $1 cm$
Show Answer
Solution:
- The given condition is shown in the figure below
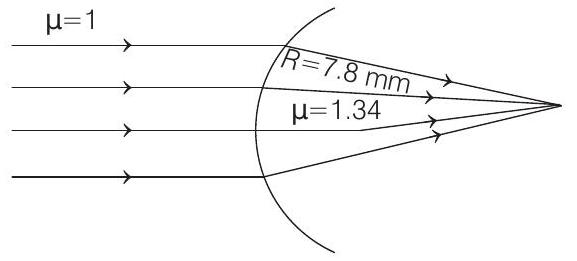
where, a parallel beam of light is coming from air $(\mu=1)$ to a spherical surface (eye) of refractive index 1.34.
Radius of curvature of this surface is $7.8 mm$.
From the image formation formula for spherical surface, i.e. relation between object, image and radius of curvature.
$$ \frac{\mu _r}{v}-\frac{\mu _i}{u}=\frac{\mu _r-\mu _i}{R} $$
Given, $\mu _r=1.34, \mu _i=1, u=\infty(-ve)$ and
$$ R=7.8 $$
Substituting the given values, we get
$$ \begin{array}{rlrl} & & \frac{1.34}{v}+\frac{1}{\infty} & =\frac{1.34-1}{7.8} \\ \text { or } & \frac{1.34}{v} & =\frac{0.34}{7.8} \\ \Rightarrow & v & =\frac{1.34 \times 7.8}{0.34} mm \\ \Rightarrow & & v & =\frac{4}{3} \times 3 \times 7.8 mm \end{array} $$
$(\because$ approximately $1.34=4 / 3$ and $0.34=1 / 3)$
$\Rightarrow$
$$ v=31.2 mm \text { or } 3.12 cm $$
