Optics 7 Question 36
37. Figure shows an irregular block of material of refractive index
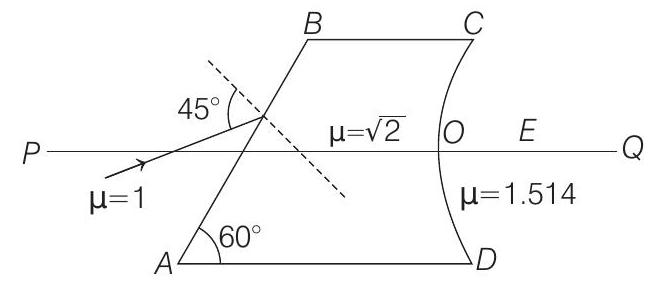
Show Answer
Solution:
- Applying Snell’s law on face
i.e. ray becomes parallel to
Now applying,
Solving this equation, we get






