Optics 7 Question 32
33. Consider a concave mirror and a convex lens (refractive index
(2015 Adv.)
When the set-up is kept in a medium of refractive index
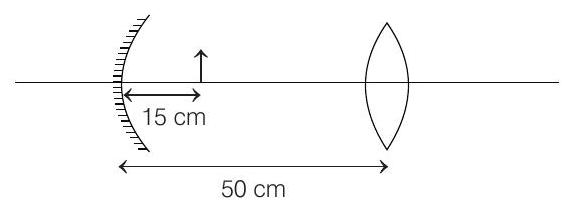
Show Answer
Solution:
- Case I
Reflection from mirror
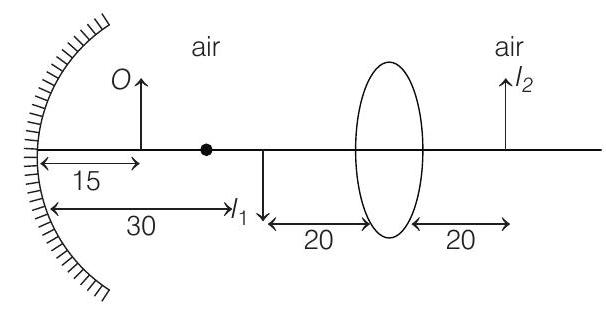
For lens
(in air)
Case II For mirror, there is no change.
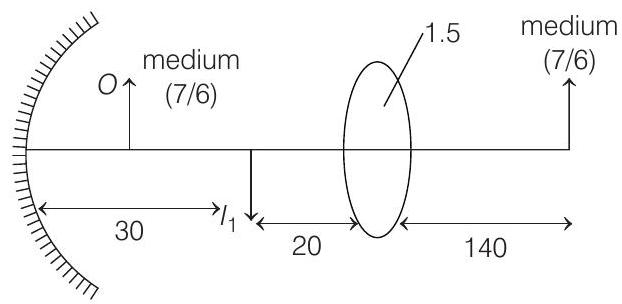
For lens,
with
We get






