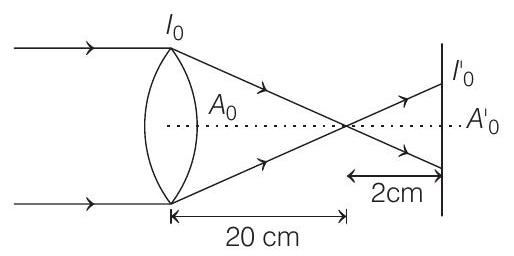
Optics 7 Question 19
19. Sunlight of intensity $1.3 kWm^{-2}$ is incident normally on a thin convex lens of focal length $20 cm$. Ignore the energy loss of light due to the lens and assume that the lens aperture size is much smaller than its focal length. The average intensity of light, in $kW m^{-2}$, at a distance $22 cm$ from the lens on the other side is
(2018 Adv.)
Passage Based Questions
Passage 1
Most materials have the refractive index, $n>1$. So, when a light ray from air enters a naturally occurring material, then by Snell’s law, $\frac{\sin \theta _1}{\sin \theta _2}=\frac{n _2}{n _1}$, it is understood that the refracted ray bends towards the normal. But it never emerges on the same side of the normal as the incident ray. According to electromagnetism, the refractive index of the medium is given by the relation, $n=\frac{c}{v}= \pm \sqrt{\varepsilon _r \mu _r}$, where $c$ is the speed of electromagnetic waves in vacuum, $v$ its speed in the medium, $\varepsilon _r$ and $\mu _r$ are the relative permittivity and permeability of the medium respectively.
In normal materials, both $\varepsilon _r$ and $\mu _r$ are positive, implying positive $n$ for the medium. When both $\varepsilon _r$ and $\mu _r$ are negative, one must choose the negative root of $n$. Such negative refractive index materials can now be artificially prepared and are called meta-materials. They exhibit significantly different optical behaviour, without violating any physical laws. Since $n$ is negative, it results in a change in the direction of propagation of the refracted light. However, similar to normal materials, the frequency of light remains unchanged upon refraction even in meta-materials.
(2012)
Show Answer
Solution:
$$ \begin{array}{rlrl} \Rightarrow \quad & \frac{A _0^{\prime}}{A _0} & =\frac{2}{20}{ }^{2}=\frac{1}{100} \\ \Rightarrow & A _0^{\prime} & =\frac{A _0}{100} \\ P & =I _0 A _0=I _0{ }^{\prime} A _0{ }^{\prime} \\ \Rightarrow & I _0^{\prime} & =\frac{I _0 A _0}{\frac{A _0}{100}} \\ & & =100 I _0=130 kW / m^{2} \end{array} $$
