Optics 7 Question 1
1. A convex lens (of focal length $20 cm$ ) and a concave mirror, having their principal axes along the same lines, are kept 80 $cm$ apart from each other. The concave mirror is to the right of the convex lens. When an object is kept at a distance of $30 cm$ to the left of the convex lens, its image remains at the same position even if the concave mirror is removed. The maximum distance of the object for which this concave mirror, by itself would produce a virtual image would be
(2019 Main, 8 April II)
(a) $25 cm$
(b) $20 cm$
(c) $10 cm$
(d) $30 cm$
Show Answer
Solution:
- The given situation can be drawn as shown below
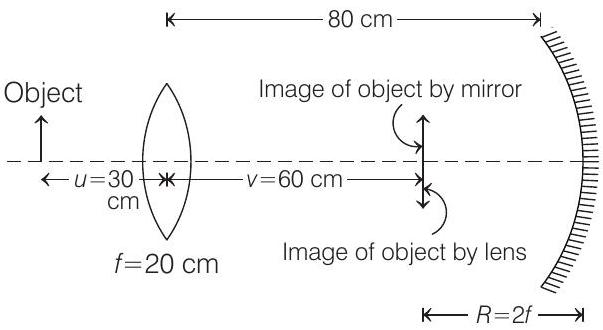
For lens formula, $\frac{1}{v}-\frac{1}{u}=\frac{1}{f}$
Substituting given values, we get
$$ \begin{aligned} \Rightarrow \quad \frac{1}{v}-\frac{1}{-30} & =\frac{1}{20} \\ v & =60 cm \end{aligned} $$
So, this image is at a distance of $80-60=20 cm$ from the mirror.
As, the image formed by the mirror coincides with image formed by the lens. This condition is only possible, if any object that has been placed in front of concave mirror is at centre of curvature, i.e. at $2 f$.
So, radius of curvature of mirror is $R=20 cm$
$\therefore$ Focal length of mirror, $f=\frac{R}{2}=10 cm$
As, for virtual image, the object is to kept between pole and focus of the mirror.
$\therefore$ The maximum distance of the object for which this concave mirror by itself produce a virtual image would be $10 cm$.
