Optics 6 Question 8
9. A planet is observed by an astronomical refracting telescope having an objective of focal length $16 m$ and an eyepiece of focal length $2 cm$
(1992, 2M)
(a) the distance between the objective and the eyepiece is $16.02 m$
(b) the angular magnification of the planet is -800
(c) the image of the planet is inverted
(d) the objective is larger than the eyepiece
Fill in the Blank
Show Answer
Solution:
- Key Idea In a YDSE, path difference between 2 rays, reaching at some common point $P$ located at angular position ’ $\theta$ ’s shown in the figure below is
$\Delta L=d \sin \theta$
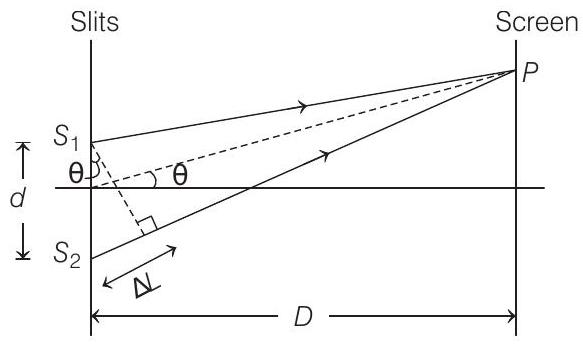
For small value of $\theta ; \sin \theta \approx \theta$
So, path difference $=\Delta L=d \theta$
For a bright fringe at same angular position ’ $\theta$ ‘, both of the rays from slits $S _1$ and $S _2$ are in phase.
Hence, path difference is an integral multiple of wavelength of light used.
$$ \begin{aligned} \text { i.e., } & \Delta L & =n \lambda \\ \text { or } & d \theta & =n \lambda \Rightarrow \lambda=\frac{d \theta}{n} \end{aligned} $$
Here, $\theta=\frac{1}{40} rad, d=0.1 mm$ Hence, $\lambda=\frac{0.1}{40 n} mm=\frac{0.1 \times 10^{-3} m}{40 n}$
$$ \begin{aligned} & =\frac{0.1 \times 10^{-3} \times 10^{9}}{40 n} n-m \\ \Rightarrow \quad \lambda & =\frac{2500}{n} n-m \end{aligned} $$
So, with light of wavelength $\lambda _1$ we have
$$ \lambda _1=\frac{2500}{n _1}(n-m) $$
and with light of wavelength $\lambda _2$, we have
$$ \lambda _2=\frac{2500}{n _2}(n-m) $$
Now, choosing different integral values for $n _1$ and $n _2$, (i.e., $n _1, n _2=1,2,3 \ldots$ etc) we find that for
$$ n _1=4, \lambda _1=\frac{2500}{4}=625 n-m $$
and for $n _2=5$,
$$ \lambda _2=\frac{2500}{5}=500 n-m $$
These values lie in given interval $500 n-m$ to $625 n-m$.
