Optics 6 Question 7
8. An astronomical telescope has an angular magnification of magnitude 5 for far objects. The separation between the objective and the eyepiece is
(1989, 2M)
(a)
(b)
(c)
(d)
Objective Question II (One or more correct option)
Show Answer
Solution:
- In the given case, figure for first minima will be as shown below
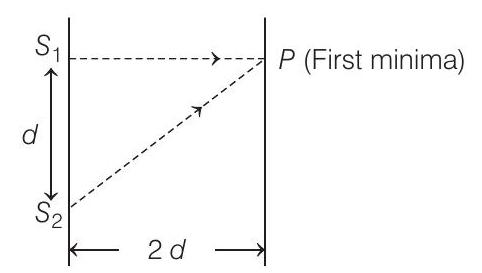
We know that condition for minima in Young’s double slit experiment is path difference,
Path difference between the rays coming from virtual sources
From triangle
and
Substituting the values from Eqs. (iii) and (iv) in Eq. (ii), we get
From Eqs. (i) and (v), we get






